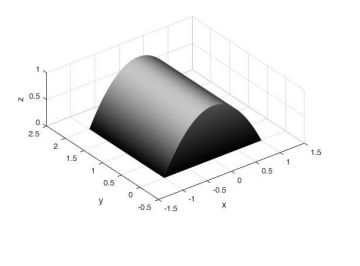
Ein Körper \( K \) sei gegeben durch
$$ K=\left\{(x, y, z) \in \mathbb{R}^{3}: x \in[-1,1], y \in[0,2], z \in\left[0,1-x^{2}\right]\right\} $$
Außerdem sei für \( a \in \mathbb{R} \) ein Vektorfeld gegeben durch:
$$ w(x, y, z)=\left(\begin{array}{c} x \\ y^{2} \\ a \end{array}\right) $$
a) Berechnen Sie den Fluss des Vektorfelds \( w \) durch die Oberfläche des Körpers \( K \) direkt,
d.h. durch Oberflächenintegrale.
Berechnung von 4 Oberflächenintegralen.
$$ \text { Dach: Parametrisierung } \Phi(x, y)=\left(\begin{array}{c} x \\ y \\ 1-x^{2} \end{array}\right),(x, y) \in D=[-1,1] \times[0,2] $$
$$ \begin{array}{c} \Rightarrow \Phi_{x}(x, y) \times \Phi_{y}(x, y)=\left(\begin{array}{c} 1 \\ 0 \\ -2 x \end{array}\right) \times\left(\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right)=\left(\begin{array}{c} 2 x \\ 0 \\ 1 \end{array}\right) \\ \iint_{\partial K_{1}} w \cdot \hat{n} d \mathcal{O}=\iint_{D} w(\Phi(x, y)) \cdot\left(\Phi_{x}(x, y) \times \Phi_{y}(x, y)\right) d(x, y) \end{array} $$ \( =\iint_{D}\left(\begin{array}{c}x \\ y^{2} \\ a\end{array}\right) \cdot\left(\begin{array}{c}2 x \\ 0 \\ 1\end{array}\right) d(x, y)=\int \limits_{0}^{2} \int \limits_{-1}^{1} 2 x^{2}+a d x d y \) \( =\int \limits_{0}^{2}\left[\frac{2}{3} x^{3}+a x\right]_{-1}^{1} d y=\int \limits_{0}^{2} \frac{4}{3}+2 a d y=\left[\left(\frac{4}{3}+2 a\right) y\right]_{0}^{2}=\frac{8}{3}+4 a \) 2. Boden: \( \Phi(x, y)=\left(\begin{array}{c}x \\ y \\ 0\end{array}\right),(x, y) \in D=[-1,1] \times[0,2], \hat{n}=\left(\begin{array}{c}0 \\ 0 \\ -1\end{array}\right) \) \( \begin{aligned} \iint_{\partial K_{2}} w \cdot \hat{n} d \mathcal{O} &=\iint_{D}\left(\begin{array}{c}x \\ y^{2} \\ a\end{array}\right) \cdot\left(\begin{array}{c}0 \\ 0 \\ -1\end{array}\right) d(x, y)=\int \limits_{0}^{2} \int \limits_{-1}^{1}-a d x d y \\ &=\int \limits_{0}^{2}[-a x]_{-1}^{1} d y=\int \limits_{0}^{2}-2 a d y=[-2 a y]_{0}^{2}=-4 a \end{aligned} \) 3. Vorderseite: \( \Phi(x, z)=\left(\begin{array}{c}x \\ 0 \\ z\end{array}\right),(x, z) \in D=[-1,1] \times\left[0,1-x^{2}\right], \hat{n}=\left(\begin{array}{c}0 \\ -1 \\ 0\end{array}\right) \) \( \iint_{\partial K_{3}} w \cdot \hat{n} d \mathcal{O}=\iint_{D}\left(\begin{array}{l}x \\ 0 \\ a\end{array}\right) \cdot\left(\begin{array}{c}0 \\ -1 \\ 0\end{array}\right) d(x, y)=\iint_{D} 0 d(x, y)=\underline{0} \) 4. Rückseite: \( \Phi(x, y)=\left(\begin{array}{c}x \\ 2 \\ z\end{array}\right),(x, z) \in D=[-1,1] \times\left[0,1-x^{2}\right], \hat{n}=\left(\begin{array}{c}0 \\ 1 \\ 0\end{array}\right) \) \( \begin{aligned} \iint_{\partial K_{4}} w \cdot \hat{n} d \mathcal{O} &=\iint_{D}\left(\begin{array}{c}x \\ 4 \\ a\end{array}\right) \cdot\left(\begin{array}{c}0 \\ 1 \\ 0\end{array}\right) d(x, y)=\int \limits_{-1}^{1} \int \limits_{0}^{1-x^{2}} 4 d z d x \\ &=\int \limits_{-1}^{1}[4 z]_{0}^{1-x^{2}} d x=\int \limits_{-1}^{1} 4-4 x^{2} d x=\left[4 x-\frac{4}{3} x^{3}\right]_{-1}^{1}=8-\frac{8}{3}=\frac{16}{3} \end{aligned} \) Insgesamt: $$ \iint_{\partial K} w \cdot \hat{n} d \mathcal{O}=\underline{8} $$
ich komme leider bei 2, 3 und 4 nicht auf \( w \) und \( \hat{n} \) , wenn ich den Boden, Vorderseite und Rückseite berechne!!
Kann bitte jemand vorrechnen, wie man auf \( w \) und \( \hat{n} \) kommt?
Und wie stellt man hierfür den Vektor: \( \Phi(x, y) \) = ?
Liebe Grüße