Ja - was ist \(\lambda\)?
Dazu (zum Einstimmen) folgender Plot
~plot~ 67.2-9x;[[-1|9|-2|45]];8*3.1;125.44/x;116.8/x;{67.2/18|33.6} ~plot~
Oben siehst Du ein Koordinatensystem, wo die horizontale Achse für den Wert \(a\) steht - also die 'Tiefe' eines Paddocks - und die vertikale Achse \(b\) die Breite aller 8 Paddocks zusammen darstellt. Der schwarze Punkt ist das errechnete Optimum \((3,73;\, 33,6)\) aus Aufgabenteil a). Die blaue Gerade beschreibt die Nebenbedingung $$N(a,b) = 9(a-0,8) + b - 60 = 0 \\ \implies b = 67,2 - 9a$$Die grüne Hyperbel beschreibt alle Paare \((a;b)\) für die die Gesamtfläche \(F=8 \cdot 15,68=124,44\) Quadratmeter wäre. Blaue Gerade und grüne Hyperbel berühren sich gerade im 'optimalen' Punkt.
Durch die Restriktion, die Boxenbreite auf \(b=3,1 \cdot 8 = 24,8\) zu beschräken (die rote Gerade), ergibt sich nun im Schnittpunkt mit der blauen Gerade (der Nebenbedingung) eine neue Lösung (s. Aufgabenteil b)). Die zugehörige Hyperbel habe ich lila eingezeichnet.
In dem Punkt der Lösung b) fallen die Steigungen der lila Flächenbedingung und der blauen Nebenbedingung nicht mehr zusammen. Es gibt einen echten Schnittpunkt. Im Gegensatz zum Punkt beim Optimum. Im Optimum darf es keinen echten Schnittpunkt geben - sonst wäre es kein Optimum; überlege mal warum!
Die Idee von Lagrange ist es, die Ableitungen der beiden Funktionen zu betrachten $$\begin{aligned}\text{grad} (F(a,b)) &= \begin{pmatrix}b\\ a\end{pmatrix} \\ \text{grad}(N(a,b)) &= \begin{pmatrix}9\\ 1\end{pmatrix} \end{aligned}$$und auszunutzen, dass im Punkt eines Optimums nur ein Berührpunkt existieren kann - d.h. diese beiden Vektoren die gleiche Richtung haben. Sie sind also linear abhängig. Falls also ein Optimum \((a_{opt};b_{opt})\) existiert, muss es dort für die Vektorgleichung$$ \text{grad} (F(a_{opt},b_{opt})) + \lambda \cdot \text{grad}(N(a_{opt},b_{opt})) = 0$$eine Lösung mit \(\lambda \in \mathbb R \backslash 0\) geben.
D.h. das \(\lambda\) ist nur ein Faktor (ein Multiplikator). Der kann im Prinzip einen beliebigen Wert (außer 0) annehmen. Man könnte ja \(N(a,b)\) mit 3 multiplizieren, was nichts ändert, aber anschließend wäre das berechnete \(\lambda\) nur ein Drittel des Wertes von vorher.
Wichtig ist also nicht der Wert von \(\lambda\) an sich, sondern dass \(\lambda\) den gleiche Wert für alle(!) Koordinaten (hier \(a\) und \(b\)) annimmt.
Ich habe versucht, das ganze noch mal in 3D darzustellen
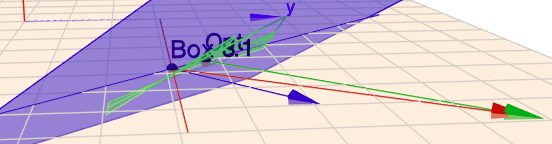
klick auf das Bild und rotiere es mit der Maus und bewege den Zoom mit dem Mausrad. Die blaue Fläche ist die Funktion \(N(a,b)\) und die grünen Segmente sollen \(F(a,b)-F_{opt}\) darstellen. Das ganze ist noch skaliert, damit es auf's Bild passt.
Wichtig sind die drei Vektoren. Der blaue Vektor zeigt den Gradienten von \(N(a,b)\), welcher unabhängig von der Position ist. Der grüne Vektor zeigt die Richtung des Gradienten im 'optimalen' Punkt. Hier läuft er parallel zum blauen. Wohingegen der Gradient bei \(b'=3,1\) (rot) von der Richtung des blauen Vektors abweicht.
Falls da noch Fragen offen sind, nur zu; melde Dich bitte
Gruß Werner