Welche Werte nehmen die Variablen x, y und h an, wenn der Inhalt der Fläche des Querschnitts mit A= 1,00 m² …

Question

Aufgabe:

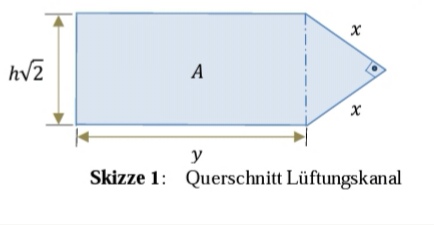
Ein Lüftungskanal hat die Querschnittsform eines Rechtecks mit aufgesetztem, gleichschenkligem Dreieck (siehe Skizze 1).

Welche Werte nehmen die Variablen x, y und h an, wenn der Inhalt der Fläche des Querschnitts mit A= 1,00 m² vorgegeben ist und zur Herstellung des Lüftungskanals der Blechverbrauch möglichst gering gehalten werden soll?

 Aus bautechnischen Gründen darf die Höhe des Kanals 1,30 m nicht überschreiten. Wie groß ist dann der Blechverbrauch in m² pro laufendem Meter Kanallänge? Bearbeitungshinweis: • Die hinreichende Bedingung muss nachgewiesen werden. • Alle Ergebnisse sollen auf 4 Nachkommastellen gerundet werden.

Problem/Ansatz:

… ich habe hier die Flächeninhalt mit X, y, h Variable geschrieben, und die gesamte Fläche ist die Summe der Fläche des Rechtecks und des gleichschenkligen Dreiecks, und ich habe die Funktion für Umfang mit diese drei Variable geschrieben, aber  das Problem ist, dass ich die Beziehung zwischen der Variablen nicht finden kann.

Answer 1

x
h^2 = x^2 + x^2
h = √ 2 * x
y

ich nehme an die Fläche links und rechts wird
nicht berücksichtigt ( Ein- und Ausfluß )

Oberfläche = 1 m^2
Ich nehme an bei deiner Aufgabenstellung wird
auch noch gefragt " Berechne das größtmögliche
Vomunen "

Dann hätte wir eine Extremwertaufgabe mit
Nebenbedingungen.

Comments

Nachtrag
Welche Werte nehmen die Variablen x, y und h an, wenn der Inhalt der Fläche des Querschnitts mit A= 1,00 m² vorgegeben ist und zur Herstellung des Lüftungskanals der Blechverbrauch möglichst gering gehalten werden soll?

Der Blechverbrauch soll doch 1 m^2 sein
.

Stell einmal ein Foto der ganzen Aufgabe
ein.

---

Danke, also muss ich die Volume berechnen, und dann mache ich Extremwertaufgabe, und nehme ich die Ein minimun Lokales, weil Lüftungskanals der Blechverbrauch möglichst gering gehalten werden soll, "das ist in Aufgabenstellung"

.

Und ist diese Funktion U = \( \sqrt{2} \) h +2y +2x

Ist das rightig?

Und danach schreibe ich diese "U" mit nur ein Variable, "wir die x- und h-Beziehung aus dem rechten Dreieck finden", und danach mach die Extremwertaufgabe und nehme ich minimun Wert der Variabl x.

Ist das rightig?

---

Wahrscheinlich nicht.
Stell´ einmal ein Foto der Aufgabe ein
oder den kompletten Originalfragetext.

---

Ja, meinen Sie die Zweite Bedingung ist, darf h 1,30 m nicht überschreiten?

---

also muss ich die Volume berechnen

Nein, du musst x, y und h berechnen.

Und ist diese Funktion U = 2√h +2y +2x
Ist das rightig?

Ja. Mittels Pythagoras kannst du h oder x eliminieren. Mittels der Nebenbedingung kannst du die zweite Variable eliminieren.

---

Ok, Ja ich muss x, y, und h berechnen, aber ich meine, dass ich die Funktion Extremwertaufgabe machen, und nehme die Lokales minimun Wert, jetzt rightig?

---

und nehme die Lokales minimun Wert, jetzt rightig?

Ja. Und zwar vom Umfang.

---

Ich entschuldige mich für die vielen Fragen, aber ich habe wirklich Problemen.

Zuerst die Fläche ist :

A= √2h.y + 1/2 x²

^{Ist das rightig?}

^{Und der Umfang ist :}

^{U = √2h + 2y + 2x}

^{Ist das rightig?}

^{Und wenn ich die Extremwertaufgabe für Umfang machen, Der Wert von h wird größer als der Wert y, und Das ist unlogisch.}

^{Und laut Pythagoras ist x= h?}

---

Zuerst die Fläche ist :
A= √2h.y + 1/2 x²
Ist das rightig?

Ja, das ist richtig.

Und der Umfang ist :

U = √2h + 2y + 2x

Ist das rightig?

Diese Frage habe ich bereits beantwortet.

Und wenn ich die Extremwertaufgabe für Umfang machen, Der Wert von h wird größer als der Wert y, und Das ist unlogisch.

Der Wert von h ist nicht größer als der Wert von y.

Und laut Pythagoras ist x= h?

Ja.

---

Der Querschnitt ist ein Rechteck plus Dreieck
Die Grundlinie hat die Länge
c = √ 2 * x
Der Abstand Spitze Dreieck zu Grundlinie
ist a = 0.7071 * x

Rechteckfläche
c * y
Dreieckfläche
c * a / 2

A = √ 2 * x * y  +  √ 2 * x * 0.7071 * x / 2
√ 2 * x * y  +  √ 2 * x * 0.7071 * x / 2 = 1

Der Umfang ist
U = y  * 2 + c + 2 * x
U = y  * 2 + √ 2 * x + 2 * x

x = 0.723 m

Ein Matheprogramm wurde zu Hilfe genommen.

Hoffentloch stimmt alles.

Ich stelle später noch eine Skizze
mit Bemaßung ein

---

Ich bedanke mich sehr, Ja ich habe alles verstanden, außer in gesamte Fläche schreiben Sie " √ 2 * x * 0.7071 * x / 2
√ 2 * x * y", also was ist das?

Wir haben die Fläche des Rechtecks und des gleichschenkligen Dreiecks, also Warum haben wir sie nicht einfach gesammelt und das hinzugefügt?

Es tut mir sehr leid für die viele Fragen, und ich danke Ihnen sehr.

---

Ich bedanke mich sehr, jetzt habe ich alles verstanden.

Und ich warte auf Skizze, ob Sie das konnen.

Danke sehr

---

Nunmehr meine hoffentlcih letzte
Variante

Der Minalumfang ist 3.912 m
Eine Kontrolle von A ergab 1 m^2

Frag nach bis alles klar ist.
Du sollst nicht unwissend sterben.

Eine Schritt für Schritt Erklärung kann
erfolgen.

---

Der Blechverbrauch soll doch 1 m^{2} sein

Der Blechverbrauch soll minimal sein, der Querschnitt soll 1 m^2 betragen.

Answer 2

Es ist

        x² + x² = (h√2)²

wegen Satz des Pythagoras.

Comments

Achso, Ich habe das rechtewinkel Symbol gesehen, aber es sieht nicht wie ein rechter Winkel aus.

Vielen Dank für Ihre Antwort.

---

Hallo oswald, die Aufgabe verwirrt mich
h*√2 = x^2 + x^2
h*√2 = 2 * x^2
h =x^2 / √2

richtig so ?

---

(h*√2)² = x² + x²

(h*√2)² = x²*2

h²*2 = x²*2

h = x