Gleichung einer Hypozykloide

Question

Aufgabe:

Text erkannt:

Aufgabe:

Wenn ein Kreis \( K_{1} \) vom Radius \( r_{1} \) innen auf einem Kreis \( K_{2} \) vom Radius \( r_{2} \) abrollt, beschreibt ein auf dem Kreisumfang von \( K_{1} \) fixierter Punkt eine sogenannte Hypozykloide.
a) Leiten Sie die Gleichung der Hypozykloide für den Fall \( r_{1}=\frac{1}{3} r_{2} \) und den Startpunkt \( x_{0}=\left(r_{2}, 0\right) \) her. Dabei seien die Mittelpunkte von \( K_{1} \) und \( K_{2} \) anfänglich (0,0) bzw. \( \left(\frac{2}{3} r_{2}, 0\right) \)
b) Fertigen Sie dazu eine Skizze an.

Problem/Ansatz:

Ich habe bereits herausgefunden, dass es das Gleiche vorgehen ist, wie wenn man einen Kreis mit Umfang \(r_{1}=r_{2}\) außen auf dem Kreis \(K_{2}\) abrollt, da der Punkt, welcher die Hypozykloide entstehen lässt sich genau auf einem solchen Kreis bewegt. (Siehe angehängte Skizze).

Es handelt sich bei der Kurve um eine um eine Kardioide mit der Gleichung:

\(x(\phi)=\frac{2}{3}*r*cos(\phi)+\frac{1}{3}*r*cos(2*\phi)\)

\(z(\phi)=\frac{2}{3}*r*sin(\phi)+\frac{1}{3}*r*sin(2*\phi)\)

Wie kann ich die Gleichung herleiten? Am liebsten wäre es mir geometrisch (über Dreiecken usw.)

Vielleicht kann mir ja jemand behilflich sein.

Comments

Startpunkt \( x_{0}=\left(r_{2}, 0\right) \)

Bist du dir da sicher? Der Punkt liegt nicht auf K₁.

---

Der Kreis \(K_2\) hat den dreifachen Umfang von \(K_1\). Folglich macht \(K_1\) drei Umdrehungen, bis er wieder am Ausgangspunkt ankommt. Die Bewegung müsste doch demzufolge etwa so aussehen - oder:

\(x_0 = (r_2,0)\) Bist du dir da sicher? Der Punkt liegt nicht auf K1.

nur wenn \(M_1(0) = (4r_1,0)\) - siehe Skizze oben. \(M_2 = (\frac 23 r_2, 0)\)

---

Ja ich bin mir sicher.

Ich hatte mich anfangs auch gewundert. Aber der Punkt muss nichts für dem Umfang von \(K_{1}\) liegen. Er dreht sich ja auch mit und erzeugt eine Kurve, wenn der Punkt innerhalb des Kreises liegt.

Ich sehe nur gerade, dass ich die Mittelpunkte der Kreise vertauscht habe.

Aber prinzipiell dache ich, man kann für die Herleitung der Gleichung auch einfach annehmen, dass der kleine graue Kreis mit Radius gleich dem von \(K_{2}\)außen um \(K_{2}\) abrollt.

---

durch den außen liegenden Kreis erhöht sich quasi die Drehfrequenz von \(K_1\).

Kannst Du nochmal verifizieren, wo genau \(M_1\) und \(M_2\) am Anfang liegen sollen. \(M_1(t=0) = (4r_1, 0)\) würde Sinn machen.

Und natürlich kann ein Punkt auf dem Umfang von \(K_1\) nicht außerhalb von \(K_2\) liegen, wenn \(K_1\) innen(!) auf \(K_2\) abrollt.

---

Ich denke, die Lage von \(M_{1}\) und \(M_{2}\)sind vertauscht. Damit würde es dann passen.
Jedoch habe ich nun absolut keine Ahnung mehr, wie die Gleichung aussehen soll und wie ich sie herleiten soll.

Answer 1

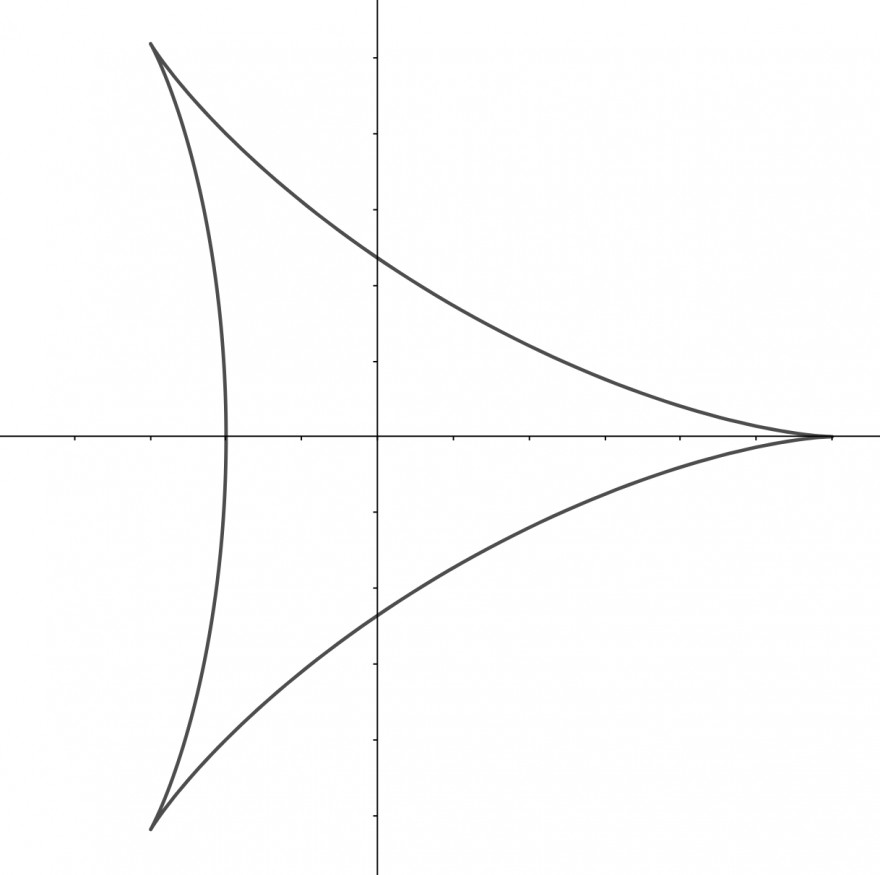
Sortieren wir also mal die Angaben:

Kreis \( K_1 \) mit Radius \( r_1 \), der Mittelpunkt \( M \) liegt am Anfang bei \( \left(\frac{2}{3}r_2,0\right) \).

Kreis \( K_2 \) mit Radius \( r_2 =3r_1 \), der Mittelpunk liegt am Anfang bei \( (0,0) \)

Auf \( K_1 \) liegt ein fixierter Punkt, nennen wir ihn mal \( P \). Zu Beginn ist \( P = (r_2,0) \)

Schauen wir uns eine Skizze an:

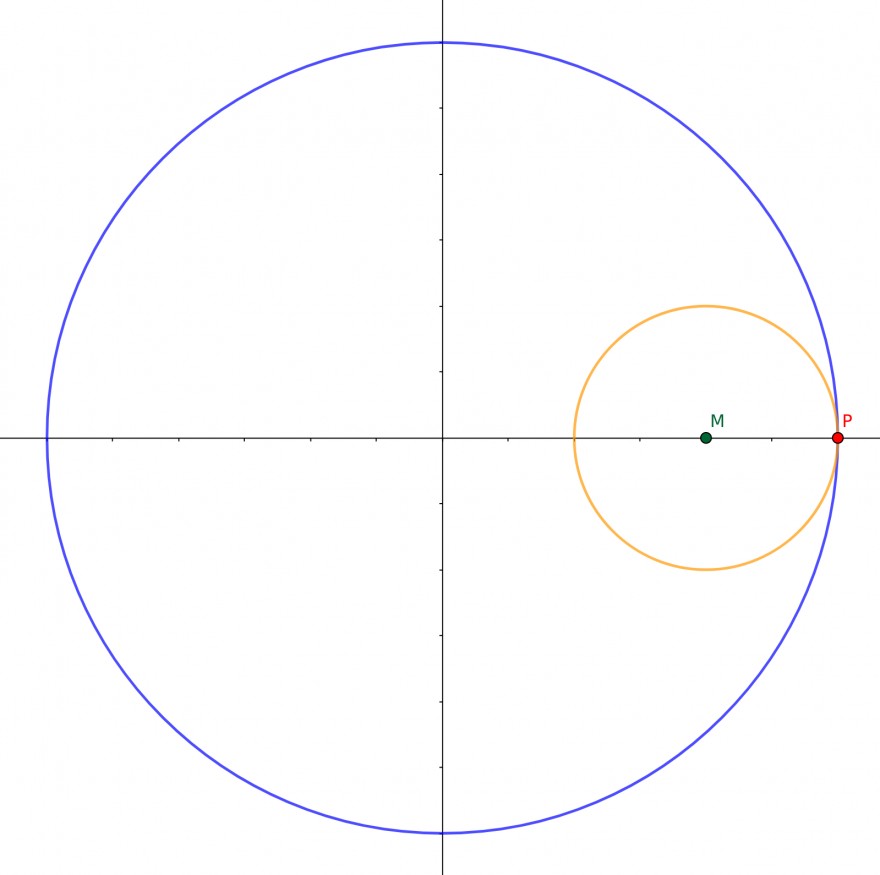
Der innere Kreis wird sich jetzt \( \frac{r_2}{r_1} = 3 \) mal abrollen, nach dem ersten mal sieht das so aus:

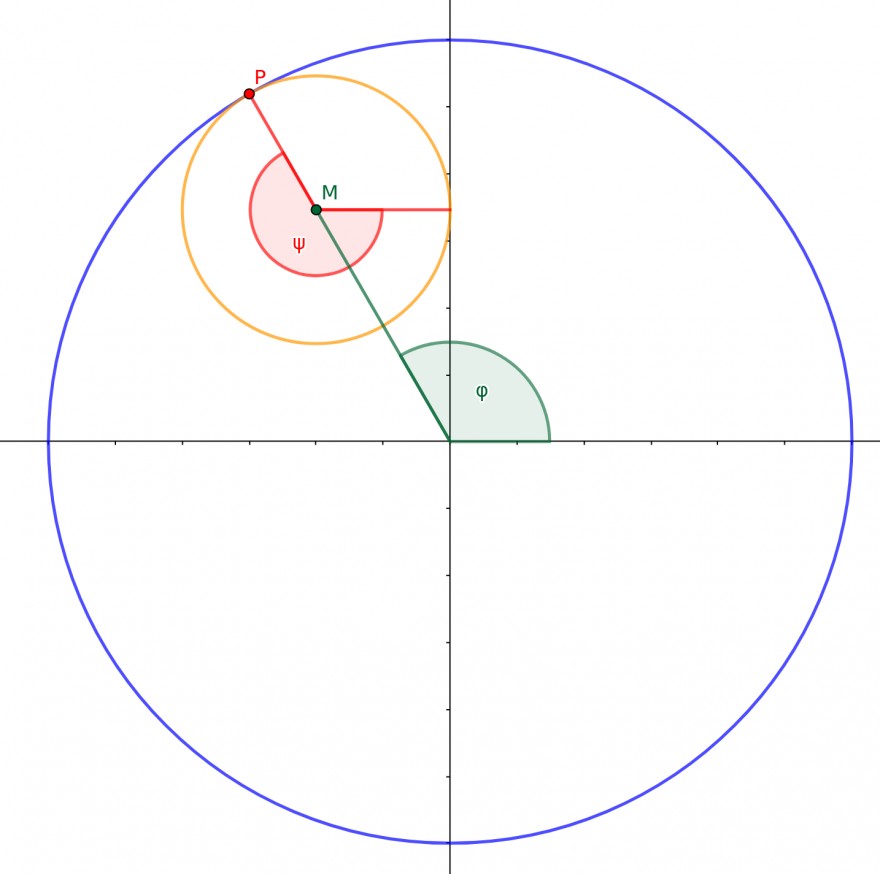
Hier gilt \( \varphi = \frac{2\pi}{3} \) und \( \psi = \frac{4\pi}{3} \) also \( \psi = 2\varphi \).

Der Weg des Mittelpunkts \( M \) wird durch die Kurve: $$ [0,2\pi) \to \mathbb{R}^2,\quad \varphi \mapsto \left( \frac{2}{3}r_2 \cos \varphi, \frac{2}{3}r_2 \sin \varphi \right) $$ beschrieben, das ist gerade ein Kreis mit Radius \( \frac{2}{3}r_2 \). Der Punkt \( P\) bewegt sich relativ zu \( M \) auf einer Kreisbahn mit Radius \( r_1 \), rotiert aber im Uhrzeigersinn. Die Kurve für die Relativbewegung lautet: $$ [0,2\pi) \to \mathbb{R}^2,\quad \varphi \mapsto r_1\left( \cos 2 \varphi, \color{blue}{\mathbf{-}} \sin 2 \varphi \right) $$  Die Absolutbewegung ist jetzt gerade die Bewegung des Mittelpunkts + der Relativbewegung zum Mittelpunkt: $$ [0,2\pi) \to \mathbb{R}^2,\quad \varphi \mapsto \left( \frac{2}{3}r_2 \cos \varphi + r_1\cos 2 \varphi, \frac{2}{3}r_2 \sin \varphi - r_1 \sin 2 \varphi  \right) $$ So sieht die Kurve aus:

Comments

$$[0,2\pi) \to \mathbb{R}^2,\quad \varphi \mapsto \left( \frac{2}{3}r_2 \cos \varphi , \frac{2}{3}r_2 \sin \varphi - \sin 2 \varphi \right)$$

IMHO: $$\varphi \mapsto \left( \frac 23 r_2 \cos \varphi {+ \frac 13 r_2 \cos 2\varphi},  \frac{2}{3}r_2 \sin \varphi - {\frac 13 r_2}\sin 2 \varphi \right)$$

---

Jup, schon korrigiert :D

Jetzt sollte hoffentlich aber alles stimmen.

Answer 2

Hallo

 sieh dir die Darstellung in geogebra an,

https://www.geogebra.org/m/u7cU8UPA

wenn du mit dem Schieber phi verstellst siehst du den Kreis abrollen.  oder lass die Animation laufen. achte auf a=r  es ist keine Kardioide.

Herleitung: auf einem Kreis um 0 mit Radius R-r, bei dir r2-r1 läuft der Mittelpunkt des Kreises mit Radius r, der muss also addiert werden, damit er abrollt muss seine Umlauffrequenz -(R-r)/r mal so groß sein .

(ersetze in deiner Gleichung in y +sin durch -sin)