Gleichung einer Epizykloide

Question

Wenn ein Kreis $K_{1}$ vom Radius $r_{1}$ außen auf einem Kreis $K_{2}$ vom Radius $r_{2}$ abrollt, beschreibt ein auf dem Kreisumfang von $K_{1}$ fixierter Punkt eine sogenannte Epizykloide.
a) Leiten Sie die Gleichung der Epizykloide für den Fall $r_{1}=r_{2}$ und den Startpunkt $x_{0}=(0,0)$ her. Dabei seien die Mittelpunkte von $K_{1}$ und $K_{2}$ anfänglich $\left(r_{1}, 0\right)$ bzw. $\left(-r_{2}, 0\right)$
b) Fertigen Sie dazu eine Skizze an.

Vielleicht kann mir ja jemand helfen.

Comments

dieser Beitrag könnte hilfreich sein.

---

Leiter hilft mir dieser Beitrag nicht wirklich.

Ich weiß, dass die Parameterdarstellung der gesuchten Epizykloide wie folgt aussieht:

$$x(\phi)=2r(1-cos(\phi))cos(\phi)$$

$$z(\phi)=2r(1-cos(\phi))sin(\phi)$$

Die Skizze ist auch kein Problem.

Einzig die Herleitung der Gleichung bereitet mir noch Probleme.

Answer 1

Hallo,

Einzig die Herleitung der Gleichung bereitet mir noch Probleme.

schau Dir dazu folgende Zeichnung an:

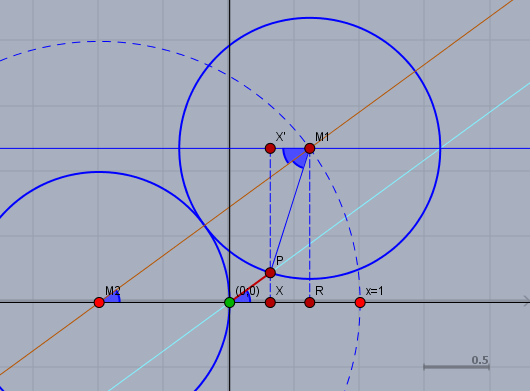
Der Kreis mit dem Mittelpunkt $M_1$ rollt auf dem Kreis links mit festem Mittelpunkt bei $M_2$ ab. Der Ursprung $O= (0,0)$ ist der grüne Punkt im Schnittpunkt der Koordinatenachsen (schwarz). Beide Kreise haben den Radius $r$ - im Bild ist $r=1$. Beachte bitte, dass das Viereck $M_2OPM_1$ ein Trapez ist, daher ist $\angle XOP = \phi= \angle XM_2M_1$. Jeder blau markierte Winkel im Bild ist $\phi$.

Für die X-Koordinate ergibt sich:$$\begin{aligned} x &= |OX| \\&= |OR| - |XR| \\&= |M_2R| - r - |XR| \\ &= 2r \cos(\phi) - r - r \cos(2\phi) \\&= 2r\left( \cos(\phi) - \frac 12(1+\cos(2\phi))\right) \\&= 2r\left( \cos(\phi) - \cos^2(\phi)\right) \\&= 2r\left( 1 - \cos(\phi)\right)\cos(\phi)\end{aligned}$$und für die Y-Koordinate gilt$$\begin{aligned}y &= |XP|\\ &= |RM_1| - |PX'| \\&= 2r\sin(\phi) - r \sin(2 \phi) \\&= 2r\sin(\phi) - 2r \cos(\phi)\sin( \phi) \\&= 2r(1-\cos(\phi))\sin(\phi) \end{aligned}$$Bei der Umwandlung habe ich von zwei Doppelwinkelfunktionen Gebrauch gemacht (siehe hier).

Falls irgendwas unklar ist, frage bitte nach.

Gruß Werner