Steckbriefaufgabe, ganzrationale Funktion vierten Grades

Question

Aufgabe:

Eine ganzrationale Funktion vierten Grades verläuft durch den Punkt P(-2|-4) und besitzt im Ursprung des Koordinatensystems ein relatives Minimum. Die Steigung ihrer Tangente an der Nullstelle x = - 1 beträgt 3.

Problem/Ansatz:

Stelle die Funktion auf

Comments

Hallo ichverstehdasnicht,
du hast jetzt 4 derselben Aufgaben
gestellt. Willst du nicht einmal versuchen
eine zu verstehen.
Am Besten durch schriftliche Lösung/
Nachrechnen.

Answer 1

$$ f(x)=ax^4+bx^3+cx^2+dx+e $$

Das sieht schwierig aus, wird aber durch die gegebenen Bedingungen einfacher.

"im Ursprung ein relatives Minimum" bewirkt d=0 und e=0, da f(0) und f'(0)=0 gilt.

Jetzt brauchst du noch drei Bedingungen.

f(-2)=-4

f(-1)=0

f'(-1)=3

usw.

Answer 2

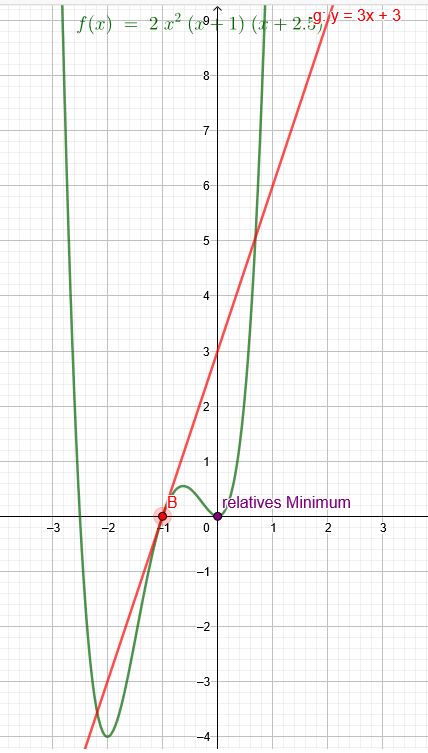
Eine ganzrationale Funktion vierten Grades verläuft durch den Punkt \(P(-2|-4)\) und besitzt im Ursprung des Koordinatensystems ein relatives Minimum. Die Steigung ihrer Tangente an der Nullstelle \(x = - 1\) beträgt 3.

Ursprung relatives Minimum  und Nullstelle \(x = - 1\)

\(f(x)=ax^2(x+1)(x-N)\)

\(P(-2|-4)\):

\(f(-2)=4a(-1)(-2-N)=-4a(-2-N)\)

\(-4a(-2-N)=-4\)  →  \(a(-2-N)=1\)  →  \(a=-\frac{1}{N+2}\) mit \(N≠-2\)

\(f(x)=-\frac{1}{N+2}[x^2(x+1)(x-N)]\)

\(f´(x)=-\frac{1}{N+2}[2x(x+1)(x-N)+x^2(x-N)+x^2(x+1)]\)

\(f´(-1)=-\frac{1}{N+2}[-2(-1+1)(-1-N)+(-1-N)+x^2(-1+1)]\)

\(f´(-1)=-\frac{1}{N+2}[(-1-N)]\)

\(-\frac{1}{N+2}[-1-N]=3\)→\(\frac{1}{N+2}[1+N]=3\)→\(N=-2,5\)       \(a=-\frac{1}{-2,5+2}\)      \(a=2\)

\(f(x)=2x^2(x+1)(x+2,5)\)