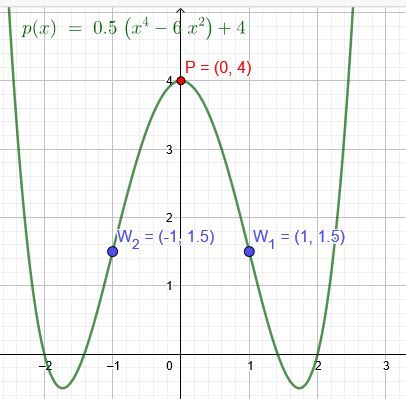
Der Graph einer ganzrationalen Funktion vierten Grades ist achsensymmetrisch zur y-Achse des Koordinatensystems. Die Wendepunkte liegen jeweils eine Einheit weit von der y-Achse und \( \frac{3}{2} \) Einheiten von der x-Achse entfernt. Ihr relatives Maximum nimmt die Funktion im Punkt \(P(0|4)\) an
Ich verschiebe den Graphen um 4 Einheiten nach unten:
Wendepunkte:\(W_1(1|1,5)\) \(W_2(-1|1,5)\)→\(W´_1(1|-2,5)\) \(W´_2(-1|-2,5)\)
relatives Maximum\(P(0|4)\)→\(P´(0|0)\)
\(f(x)=ax^2(x-N)(x+N)=ax^2(x^2-N^2)=a(x^4-N^2x^2)\)
\(W´_1(1|-2,5)\):
\(f(1)=a(1-N^2)\) → \(a(1-N^2)=-2,5\) → \(a(N^2-1)=2,5\) → \(a=\frac{2,5}{N^2-1}\) mit \(N≠±1\)
\(f(x)=\frac{2,5}{N^2-1}(x^4-N^2x^2)\)
\(f'(x)=\frac{2,5}{N^2-1}(4x^3-2N^2x)\)
\(f''(x)=\frac{2,5}{N^2-1}(12x^2-2N^2)\)
\(f''(1)=\frac{2,5}{N^2-1}(12-2N^2)\)
\(\frac{2,5}{N^2-1}(12-2N^2)=0\)
\(N^2=6\) \(a=0,5\)
\(f(x)=0,5(x^4-6x^2)\)
Ich verschiebe den Graphen um 4 Einheiten nach oben:
\(p(x)=0,5(x^4-6x^2)+4\)