Funktionenschar f(x):= x^4 - k x^2 mit x ∈ ℝ und Parameter k > 0 Parameter

Question

wir haben ein neues Thema und ich bräuchte Hilfe bei diesen Aufgaben:

Funktion: f(x) = \( x^{4} \) - k \( x^{2} \)  mit x ∈ ℝ  und k > 0

a)Zeigen Sie, dass sich alle Funktionen der Funktionsschar im Ursprung berühren.

b)Untersuchen Sie die Funktionsschar f allgemein nach dem zuvor angegebenen Schema und skizzieren Sie die Funktionen der Schar für k = 1 und k = 2 gemeinsam in einem Koordinatensystem.

c)Bestimmen Sie die Funktion g, die die Ortslinie aller Extrempunkte beschreibt.

d)Bestimmen Sie die Funktion h, die die Ortslinie aller Wendepunkte beschreibt.

e)Welche Funktion der Funktionsschar hat bei x = 2 eine Nullstelle?

f)Welche Funktion der Funktionsschar hat bei x = 3 einen Tiefpunkt?

g)Welche Funktion der Funktionsschar hat bei x = 3 einen Wendepunkt?

Bitte helfen!

Answer 1

Hallo,

a)Zeigen Sie, dass sich alle Funktionen der Funktionsschar im Ursprung berühren

Setzte für f(x) und x null ein und schaue, ob sich eine wahre Aussage ergibt.

b)Untersuchen Sie die Funktionsschar f allgemein nach dem zuvor angegebenen Schema und skizzieren Sie die Funktionen der Schar für k = 1 und k = 2 gemeinsam in einem Koordinatensystem.

Nach welchem Schema sollt ihr vorgehen? Nullpunkte, Extrem- und Wendestellen berechnen?

Die Skizzen sehen so aus:

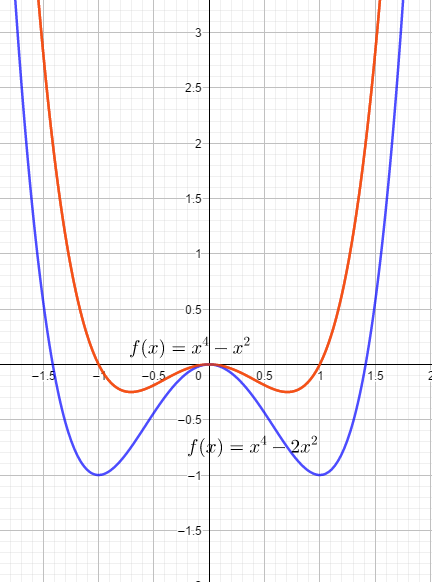
c)Bestimmen Sie die Funktion g, die die Ortslinie aller Extrempunkte beschreibt.

Nachdem du die Extrempunkte in Abhängigkeit von k bestimmt hast, stellst du die Extremstelle nach k um und setzt das in die Ausgangsgleichung ein.

Genauso gehst du bei d) für die Ortslinie der Wendepunkte vor.

e)Welche Funktion der Funktionsschar hat bei x = 2 eine Nullstelle?

Du setzt  die Ausgangsgleichung gleich null und gleichzeitig für x 2 ein und löst nach k auf.

f)Welche Funktion der Funktionsschar hat bei x = 3 einen Tiefpunkt?

Du setzt die 1. Ableitung = 0 und für x 3 ein, dann nach k auflösen und das Ergebnis in die 2. Ableitung einsetzen, um zu prüfen, ob es sich um einen Hoch- oder Tiefpunkt handelt.

Gleiches Vorgehen bei h), hier dann die 2. Ableitung = 0 und für x 3 einsetzen.

Melde dich bitte, wenn du weitere Hilfe brauchst.

Gruß, Silvia

Comments

Wie berechne ich die Extrempunkte und Wendepunkte? Bei einer normalen Funktion hätte ich es ja auch alleine geschaft aber hier ist ein “k”

und bei b) ist das glaube ich eine vollständige Funktionsuntersuchung, Nullstellen, Wertemenge, Defnitionsmenge, Wertetabelle undso....

---

Behandle das k einfach wie eine Zahl. In deinen Ergebnissen wird das k immer vorkommen.

z.B. die Nullstellen:

\(x^4-kx^2=0\\ x^2\cdot(x^2-k)=0\\ x_1=0\quad∨x^2-k=0\\x_1=0\quad ∨ x^2=k\\ x_1=0, x_2=\sqrt{k},x_3=-\sqrt{k}\)

So gehst du auch bei den Extrem- und Wendepunkten vor.

---

Bestimmung der Ortslinie für den Tiefpunkt \(TP_1(\sqrt{0,5k}|-0,25k^2)\):

\(x=\sqrt{0,5k}\\ x^2=0,5k\\2x^2=k\)

In die Ausgangsgleichung einsetzen:

$$O(x)=x^4-(2x^2)^2\\O(x)=x^4-2x^4\\O(x)=-x^4$$

---

Dankeschön! :)