Partition für Obersumme

Question

ÜBuNG 5.27. - Zeigen Sie, dass die Funktion \( g:[0,1] \rightarrow[0,1] \), gegeben durch
$$ g(x)=\left\{\begin{array}{ll} 0 & \text { falls } x \text { irrational oder } x=0 \\ \frac{1}{q} & \text { falls } x=\frac{p}{q} \text { mit } p, q \text { teilerfremd } \end{array}\right. $$
integrierbar ist. Als Hilfestellung stellen wir den Graphen dar, aber überlassen Ihnen die Interpretation des Graphen und die sich daraus ergebenden Überlegungen.

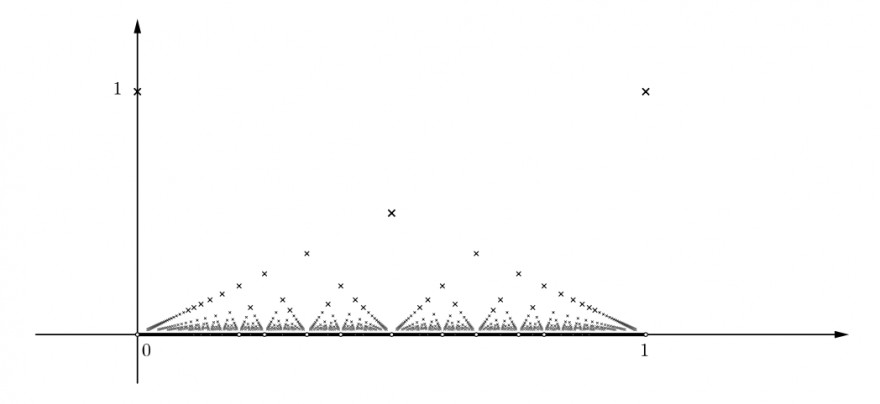
Welche Partition muss ich für die Obersumme wählen ?

Answer 1

Das ist die Thomaesche Funktion. Sie ist an allen irrationalen Stellen stetig. Sie hat also nur abzählbar viele Unstetigkeitsstellen. Nach dem Lebesgue-Kriterium für Riemann-Integrierbarkeit ist \(g\) deshalb Riemann-integrierbar.