Dichtefunktion Erwartungswert bestimmten

Question

Aufgabe:

Ich habe schon mal eine Frage dazu gepostet, aber jetzt etwas spezifischer:

Text erkannt:

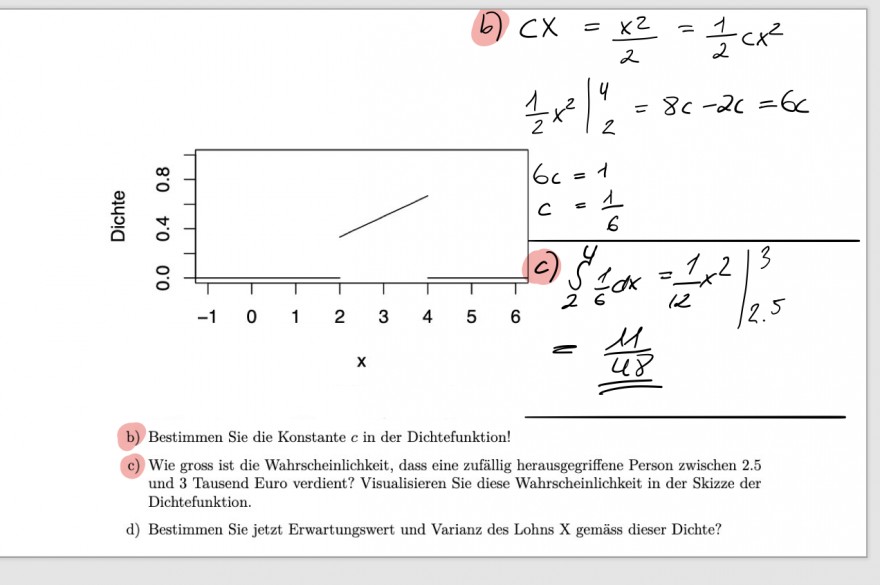
$b=\frac{x^{2}}{2}=\frac{1}{2} c x^{2}$
b) Bestimmen Sie die Konstante $c$ in der Dichtefunktion!
c) Wie gross ist die Wahrscheinlichkeit, dass eine zufällig herausgegriffene Person zwischen 2.5 und 3 tausend Euro verdient? Visualisieren Sie diese Wahrscheinlichkeit in der Skizze der
Dichtefunktion.
d) Bestimmen Sie jetzt Erwartungswert und Varianz des Lohns X gemäss dieser Dichte?

Problem/Ansatz:

a und b wären geklärt.

Jetzt geht es um die c.

Die Lösung sieht so aus:

Text erkannt:

$E(x)=\int \limits_{-\infty}^{\infty} x \cdot f(x) d x=\int \limits_{-\infty}^{2} 00 x+\int \limits_{2}^{4} \frac{1}{6} x^{2}+2$
$\int \limits_{4}^{\infty} 0 d x=\int \limits_{2}^{4} \frac{1}{6} x^{2} d x$
$E(x)=\int \limits_{2}^{4} \frac{1}{6} x^{2} d x=\left.\frac{1}{18} x^{3}\right|_{2} ^{4}=\frac{56}{18}$
$=3.111$

Wie kommt man auf einmal auf 1/6x²?? Von 1/6x ? Ich bin also ab der gelb markierten stelle raus. Ich verstehe irgendwie nur Bahnhof ab dieser Aufgabe. Danke für jegliche Hilfe!

Comments

Vom Duplikat:

Titel: Bestimmen Sie die Konstante c in der Dichtefunktion.

Stichworte: statistik

Aufgabe:

In einem Betrieb verdienen Mitarbeitende zwischen 2000 und 4000 Euro brutto. Es sei: X ~ “Lohn in Tausend Euro”
Diese als stetig angenommene Lohnstruktur kann durch folgende Dichtefunktion f(x) beschrieben werden:

Problem/Ansatz:

Bestimmen Sie die Konstante c in der Dichtefunktion. 

Ich hab die Lösung eigentlich dazu aber ich kann es nicht nachvollziehen. Die Lösung wäre am ende: 1/6.

also 8c - 2c = 6c. Steht am kommt man auf 1/6x. Ich würde aber niemals darauf kommen. Kann mir da jemand sagen wie man im einzelnen voran geht?

Answer 1

Bestimmen Sie die Konstante c in der Dichtefunktion. 

Das Integral der Dichtefunktion ist 1. Laut Definition. Sonst ist es keine Dichtefunktion.

Also ist der Flächeninhalt unter der Dichtefunktion 1.

Die Fläche ist ein Trapez mit parallelen Seiten der Länge f(2) und f(4) und einer Höhe von 4-2 = 2.

Gemäß Formel für den Flächeninhalt eines Trapezes ergibt das einen Flächeninhalt von (4c + 2c)/2 · 2 und somit die Gleichung

        (4c + 2c)/2 · 2 = 1.

Answer 2

∫ (2 bis 4) (c·x) dx = 1 --> c = 1/6

Schaffst du es selber die Gleichung zu lösen? Wenn nicht woran hängst du fest?

Denke daran. Du kannst das Integral ersetzen

∫ (a bis b) f(x) dx = F(b) - F(a)

Comments

Ich schaffe es nicht die Gleichung zu lösen

---

Ich schaffe es nicht die Gleichung zu lösen

Wenn du es nicht schaffst solltest du eigentlich sagen wo du hängen bleibst.

f(x) = c·x

F(x) = 1/2·c·x²

∫ (2 bis 4) (c·x) dx = 1

(1/2·c·4²) - (1/2·c·2²) = 1

8·c - 2·c = 1

6·c = 1

c = 1/6

---

Wie kommt man auf einmal auf 1/6x^2?? Von 1/6x ?

Genau. Was ist f(x)? Und was ist demnach x·f(x)?

---

Aha ich habs denke ich. 1/6x * x = 1/6x²

---

Genau. Richtig erkannt.