Hallo,
Das ist meine Formel:
let det = (mX-qX)*(pY-qY)-(mY-qY)*(pX-qX);
Die Formel ist korrekt und Du solltest hier unterschiedliche Vorzeichen bekommen, wenn \(P\) einmal links und einmal rechts der Geraden liegt.
Ist der Punkt rechts dann ist Ergebnis +, wenn links dann -
Es ist umgekehrt. Nimmst Du den Vektor \(\vec{QM} = M-Q\) als Bezugrichtung, so stehen dessen Koordinaten in der ersten Spalte der 2x2-Matrix, von der die Determinante berechnent wird. Dann gilt: $$(M-Q)\times (P-Q) \\ \quad = \left|\begin{array}{} m_x-q_x & p_y-q_y \\ m_y-q_y & p_y-q_y \end{array}\right| = \begin{cases} \gt 0, \quad p \space \text{links}\\ < 0, \quad p\space \text{rechts}\end{cases}$$Das 'links' und 'rechts' bezieht sich auf die Richtung von \(\vec{QM}=M-Q\). So als ob man sich auf den Punkt \(Q\) stellt und nach \(M\) blickt. Hier mal ein Beispiel:
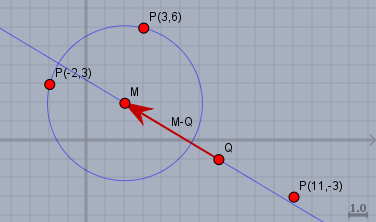
$$M = \begin{pmatrix}2\\ 2\end{pmatrix}, \quad Q = \begin{pmatrix}7\\ -1\end{pmatrix}, \quad M-Q=\begin{pmatrix}m_x-q_x\\ m_y-q_y\end{pmatrix} = \begin{pmatrix}-5\\ 3\end{pmatrix} \\ P = \begin{pmatrix}3\\ 6\end{pmatrix} \implies P-Q = \begin{pmatrix}p_x-q_x\\ p_y-q_y\end{pmatrix}= \begin{pmatrix}-4\\ 7\end{pmatrix} \\ (m_x-q_x)\cdot (p_y-q_y)-(m_y-q_y)\cdot (p_x-q_x) \\ \quad = -5 \cdot 7 - 3 \cdot (-4) = -35+12 = -23 \lt 0 $$rechne es ruhig mal für die anderen beiden Punkte in der Skizze nach:$$P_{(-2,3)} \to (M-Q) \times (P_{(-2,3)}-Q) = 7 \gt 0 \to \text{links}\\ P_{(11,-3)} \to (M-Q) \times (P_{(11,-3)}-Q) = -2 \lt 0 \to \text{rechts}$$Solltest Du immer das gleiche Vorzeichen bekommen, liegt Dein Problem außerhalb dieser Code-Zeile.
Wenn Du den Winkel \(\angle QMP\) berechnen möchtest, sieht die Sache leicht anders aus. Um einen Winkel zu bestimmen, betrachtet man die beiden Vektoren, die vom Scheitel des Winkels ausgehen:
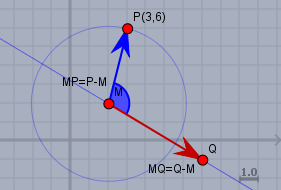
Im Falle des Winkels \(\angle QMP\) (blau) ist der Scheitel \(M\) und die beiden Vektoren sind \(\vec{MQ} = Q-M\) (die Bezugsrichtung; rot) und \(\vec{PM}\) (der 'freie' Schenkel; blau). In der Skizze oben ist$$\vec{MQ} = \begin{pmatrix}5\\ -3\end{pmatrix}, \quad \vec{MP} = \begin{pmatrix}1\\ 4\end{pmatrix}$$Weiter ist dann$$\vec{MQ} \times \vec{MP} = \left|\begin{array}{cc}5& 1\\ -3& 4\end{array}\right| = 23 \\ \vec{MQ} \cdot \vec{MP} = (q_x-m_x)(p_x-m_x) + (q_y-m_y)(p_y-m_y)\\ \quad = 5 \cdot 1 + (-3) \cdot 4 = -7$$Die zweite Zeile ist das Skalarprodukt der Vektoren. Die meisten Programmiersprachen verfügen über eine Funktion arctan2, die aus diesen beiden Werten den Winkel zwischen den Vektoren berechnent. In Javascript ist das Math.atan2(y,x):$$\text{Math.atan2}(23,-7) \approx 1,866 \equiv 106,9°$$Das Ergebnis ist ein Wert im Bogenmaß (rad) zwischen \(-\pi\) und \(\pi\). Der Wert ist wieder positiv, wenn \(P\) auf der linken Seite von \(\vec{MQ}\) liegt. Da sich hier aber zu dem Bild vorher die Blickrichtung geändert hat, haben sich auch die Seiten links und rechts vertauscht. Achte bei atan2 darauf, wo Du welchen Wert einträgst. Bei Javascript kommt zuerst der Wert aus der 'Determinante' (nennt sich dort y-Wert). Excel kennt die Funktion auch, nur dort sind die Parameter vertauscht.
... und wie immer gilt: falls noch was unklar ist, bitte melden.