Ganz unten:Achtung bei r=... fehlt das pi -> somit auch bei der Höhe h!!!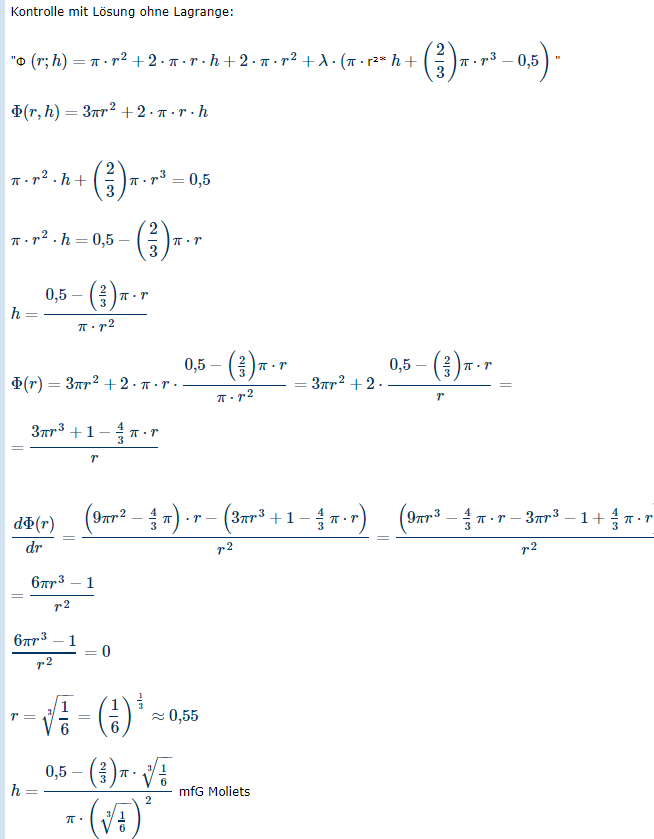
Text erkannt:
Kontrolle mit Lösung ohne Lagrange:
\( " \Phi(r ; h)=\pi \cdot r^{2}+2 \cdot \pi \cdot r \cdot h+2 \cdot \pi \cdot r^{2}+\lambda \cdot\left(\pi \cdot r^{2} * h+\left(\frac{2}{3}\right) \pi \cdot r^{3}-0,5\right) \)
\( \Phi(r, h)=3 \pi r^{2}+2 \cdot \pi \cdot r \cdot h \)
\( \pi \cdot r^{2} \cdot h+\left(\frac{2}{3}\right) \pi \cdot r^{3}=0,5 \)
\( \pi \cdot r^{2} \cdot h=0,5-\left(\frac{2}{3}\right) \pi \cdot r \)
\( h=\frac{0,5-\left(\frac{2}{3}\right) \pi \cdot r}{\pi \cdot r^{2}} \)
\( \Phi(r)=3 \pi r^{2}+2 \cdot \pi \cdot r \cdot \frac{0,5-\left(\frac{2}{3}\right) \pi \cdot r}{\pi \cdot r^{2}}=3 \pi r^{2}+2 \cdot \frac{0,5-\left(\frac{2}{3}\right) \pi \cdot r}{r}= \)
\( =\frac{3 \pi r^{3}+1-\frac{4}{3} \pi \cdot r}{r} \)
\( \frac{d \Phi(r)}{d r}=\frac{\left(9 \pi r^{2}-\frac{4}{3} \pi\right) \cdot r-\left(3 \pi r^{3}+1-\frac{4}{3} \pi \cdot r\right)}{r^{2}}=\frac{\left(9 \pi r^{3}-\frac{4}{3} \pi \cdot r-3 \pi r^{3}-1+\frac{4}{3} \pi \cdot r\right.}{r^{2}} \)
\( =\frac{6 \pi r^{3}-1}{r^{2}} \)
\( \frac{6 \pi r^{3}-1}{r^{2}}=0 \)
\( r=\sqrt[3]{\frac{1}{6}}=\left(\frac{1}{6}\right)^{\frac{1}{3}} \approx 0,55 \)
\( h=\frac{0,5-\left(\frac{2}{3}\right) \pi \cdot \sqrt[3]{\frac{1}{6}}}{\pi \cdot\left(\sqrt[3]{\frac{1}{6}}\right)^{2}} \) mfG Moliets