Hallo,
Aber mein Problem ist, dass ich nicht weiß wie man auf a, b und c kommt um den Cosinussatz anwnden zu können.
was wahrscheinlich daran liegt, dass Du keine Zeichnung gemacht hast. Z.B. so eine, wie diese hier:
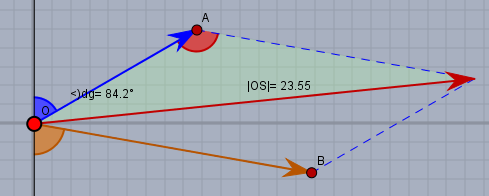
Schlepper \(A\) zieht mit der blauen Kraft im blauen Winkel von \(60°\) und Schlepper \(B\) mit der braunen Kraft im braunen Winkel von \(80°\). Beide Kräfte spannen ein Parallelogramm auf und die Diagonale (rot) ist die Resultierende Kraft.
Im markierten Dreieck kannst Du den Cosinussatz anwenden:$$\alpha = 80° + 60° \\ b = 15 \text{kN} \\ c = 10 \text{kN}$$Dein Ergebnis kannst Du in der Zeichnung kontrollieren.
Deine Überschrift enthält: "Rechnen mit Vektoren". Die Anwendung des Kosinussatzes gehört i.A. nicht dazu. Das erste, was Du zum Rechnen mit Vektoren benötigst, ist ein Koordinatensystem, bzw. dessen Festlegung. Um auf das gewünschte Ergebnis zu kommen solltest Du die erste Koordinatenrichtung nach oben (Norden) und die zweite nach rechts (Osten) wählen. Das ist nicht unbedingt üblich, aber die Angaben in der Aufgabe und in der Lösung sind auch ziemlich unüblich!
Du solltest Dir vielleicht noch merken, dass mit der Wahl dieses Koordinatensystems die Winkel im Uhrzeigersinn positiv drehen.
Ist ein Vektor \(\vec v\) mit seinem Betrag \(|\vec v|\) und seinem Richtungswinkel \(\varphi\) gegeben, so lautet er in Koordinatenscheibweise$$\vec v = |\vec v| \cdot \begin{pmatrix} \cos \varphi\\ \sin \varphi\end{pmatrix}$$Damit lauten die Zugvektoren der beiden Schlepper$$\begin{aligned} \vec a &= 10 \text{kN} \cdot \begin{pmatrix} \cos 60°\\ \sin 60°\end{pmatrix} \approx \begin{pmatrix}5.00\\ 8.66\end{pmatrix} \text{kN}\\ \vec b &= 15 \text{kN} \begin{pmatrix} \cos (180° - 80°)\\ \sin (180° - 80°) \end{pmatrix} \approx \begin{pmatrix}-2.60\\ 14.77\end{pmatrix} \text{kN}\end{aligned}$$Wenn Dir unklar ist, warum bei \(\vec b\) der Winkel von 180° abgezogen wird, so frage bitte nach.
Und für die resultierende Kraft \(\vec r\) muss man beide nur addieren:$$\vec r = \begin{pmatrix}5.00\\ 8.66\end{pmatrix} \text{kN} + \begin{pmatrix}-2.60\\ 14.77\end{pmatrix} \text{kN} = \begin{pmatrix}2.40\\ 23.43\end{pmatrix}\text{kN}$$Der Betrag der Kraft berechnet sich nach Pythagoras aus der Wurzel der Quadratesumme der Koordinaten$$|\vec r| = \sqrt{r_1^2 + r_2^2} \approx 23,55 \text{kN}$$und der Winkel (hier gegenüber Nord) aus dem Arcustangens der Koordinaten$$\varphi_r = \arctan\left( \frac {r_2}{r_1}\right) \approx \arctan\left( \frac {23,43}{2,4}\right) \approx 84,16°$$bei letzteren gilt es noch auf die Vorzeichen zu achten, sobald sich der Vektor nicht mehr im ersten Quadranten befindet.