Moin Leute!
Die Aufgabenstellung lautet:
In der hier dargestellten Abbildung ist der Querschnitt eines Blasebalgs zu sehen. Dieser besteht aus 5 identischen Falten, deren Querschnitte gleichschenklige Dreiecke sind. Wie groß ist die äußere Oberfläche des Blasebalgs für \( D_{i}=3 c m, D_{a}=5 \mathrm{cm} \) und \( \mathrm{H}=12 \mathrm{cm} ? \)
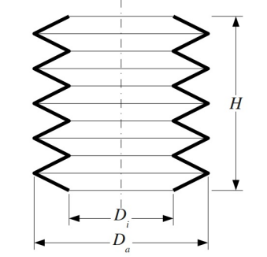
Ich sehe, dass es sich hierbei um einen Rotationskörper handelt. Was ich machen würde ist, erstmal den Körper in gleichgroße Zehntel aufzuteilen (wie in der Skizze angedeutet), die Fläche von einem der Zehntel zu berechnen und dann *10 rechnen. Die Kurve ist dann einfach ein gerades Stück, z.B. von z=0 bis zum ersten Knick bei z=H/10, an dem der Durchmesser Da ist.
Was ich momentan nicht hinbekomme, ist die Kurve aufzustellen und ihren Schwerpunkt zu bestimmen. Mein Ansatz ist
c(h)= \( \begin{pmatrix} r\\h \end{pmatrix} \) = \( \begin{pmatrix}\frac{D_i}{2} + \frac{D_a-D_i}{2}*\frac{10h}{H}\\h \end{pmatrix} \) wobei h ∈ [0,\( \frac{H}{10} \)] und r (hoffentlich) = [\( \frac{D_i}{2} \),\( \frac{D_a}{2} \)]
So wie ich den Prof verstanden habe, kann ich an dieser Stelle die erste Guldinsche Regel verwenden:
\( |S|=2 \pi \int \limits_{c} x=2 \pi x_{s} \cdot|c| \)
Das |c| bekomme ich über den Satz des Pythagoras mit ca. 1,56 cm.
Und das Integral würde ich wie folgt berechnen:
\( \int\limits_{0}^{H/10}\) \( \int\limits_{R_i}^{R_i+(R_a-R_i)*\frac{10h}{H}} \) 1dr dh, wobei ich hier D_i/2 und D_a/2 übersichtshalber durch die Radien R_i, R_a ersetzt habe.
Die letzte Zeile vor dem Einsetzen der Werte lautet bei mir:
(Ra - Ri) *\( \frac{5h^2}{H} \)|0 H/10
Hier sieht man schon, dass das Ergebnis eine Fläche sein wird. Ich vermute, es liegt an meinen Grenzen für r. Ich wüsste aber nicht, wie ich sie anders wählen müsste.
Ich glaube, ich stelle mich einfach nur extrem dumm an aber kann mir eventuell trotzdem jemand beim Schwerpunkt helfen und allgemein mein Ansatz beurteilen?
Würde mich über jede Hilfe freuen.