Hallo,
zu (a) .. um diese blaue Fläche geht es:
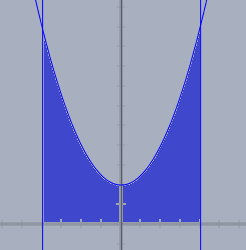
... und die ist $$F = \int_{-2}^{+2} x^2 + 1\,\text dx = \left.\frac 13 x^3 + x \right|_{-2}^{+2} \\\phantom{F} = \frac{14}3 - \left( \frac{14}3\right) = \frac{28}3$$
bei (b) ist wichtig zu beachten, dass sich der Graph um die Y-Achse drehen soll. Damit nimmt der Körper hier die Form eines (heraus geschnittenen) Paraboloiden an.
Denkt man sich aus diesem Körper eine waagerechte Scheibe heraus geschnitten (oberhalb von \(y=1\)), so besteht diese aus einem Kreisring mit Außenradius \(2\) und Innenradius \(x\). Das sieht etwa so aus:
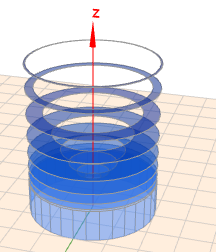
Die Fläche \(F_R\) so eines Rings ist $$F_R = \pi \cdot 2^2 - \pi \cdot x^2 = \pi(4-x^2)$$Die Höhe eines Rings sei \(\text dy\) und die Summe aller Ringe gibt das Volumen \(V_2\) ab \(y=1\) aufwärts$$V_2 = \int_{y=1}^{y=y(2)} F_R \,\text dy $$Aus der Funktion für \(y\) folgt $$y = x^2 + 1 \implies x^2 = y-1 $$Einsetzen gibt dann$$\begin{aligned}V_2 &= \int_1^{5} \pi(4 - (y-1))\, \text dy \\&= \pi \int_1^5 (5-y)\,\text dy = \pi\left[5y - \frac 12 y^2 \right]_1^5 \\ &=\pi\left( \frac{25}2 - \frac 92\right) = 8\pi\end{aligned}$$Jetzt noch das Volumen \(V_1=\pi r^2h\) des Zylinders unterhalb von \(y=1\) dazu zählen gibt dann das gesuchte Volumen \(V\)$$ V = V_1 + V_2 = \pi \cdot 2^2 \cdot 1 + 8\pi = 12\pi$$
(c) ist jetzt einfach - oder? \(h' = 3\)
(d) die Bogenlänge \(s\) ist die Summe aller Bogenstücke \(s = \int \text ds\). So ein Bogenstück ist nach Pythagoras$$\text ds^2 = \text dx^2 + \text dy^2 =\left( 1 + \left(\frac{\text dy}{\text dx} \right)^2\right) \text dx^2 \\\implies \text ds = \sqrt{ 1 + \frac{\text dy}{\text dx}}\, \text dx = \sqrt{1 + y'^2}\, \text dx$$und mit \(y' = 2x\) wird dann aus \(s\)$$\begin{aligned}s &= \int_{-2}^{2} \sqrt{1 + (2x)^2}\, \text dx \\&= \left. \frac x2 \sqrt{1+4x^2} + \frac 14 \text{arcsinh}(2x) \right|_{-2}^{+2}\\&= \left. \frac x2 \sqrt{1+4x^2} + \frac 14 \ln\left(2x+\sqrt{1+4x^2}\right) \right|_{-2}^{+2} \\&\approx 9,29\end{aligned}$$
(e) die größte Hürde ist hier, die Oberfläche des Paraboloidenstückes zu berechnen. Man denke sich wieder, dass das Volumenstück und damit die auch die Mantelfläche in infinitisemal dünne Scheiben geschnitten. Der Umfang einer solchen Scheibe ist dann der eines Kreises mit Radius \(x\) also \(2x\pi\) und die 'Höhe' ist das \(\text ds\) von oben. Also ist die Oberfläche \(O_P\) des Paraboloiden $$O_P = \int_{y=1}^{5} 2x\pi \,\text ds$$Hier muss nun \(x\) und \(\text ds\) in Abhängigkeit zu \(y\) gebracht werden. Es ist$$y = x^2+1 \implies x = \sqrt{y - 1 } \\ \text ds = \sqrt{ 1 + \left(\frac{\text dx}{\text dy} \right)^2} \,\text dy \\ \frac{\text dx}{\text dy} = \frac 1{2\sqrt{y-1}}$$Wie üblich alles das in das Integral für \(O_P\) einsetzen$$\begin{aligned}O_P &= \int_{y=1}^{5} 2x\pi \,\text ds \\&= \int_{y=1}^{5} 2 \sqrt{y - 1 }\pi \sqrt{ 1 + \frac{1}{4(y-1)}} \,\text dy \\&= \pi\int_{y=1}^{5} \sqrt{y-1 }\sqrt{ 4 + \frac{1}{(y-1)}} \,\text dy\\&= \pi\int_{y=1}^{5} \sqrt{4y-3 } \,\text dy \\ &= \pi \left[ \frac 16 \sqrt{(4y-3)^3}\right]_1^5 \\&= \frac{\pi}6\left( \sqrt{17^3}-1\right) \approx 36,2 \end{aligned}$$Addiere dazu noch den Zylindermantel \(O_M\) und die Grundfläche \(O_G\)$$r = 2 \\ h=y(2)=5 \\ O_M=2\pi rh = 20\pi \\ O_G = \pi r^2 = 4\pi$$
Gruß Werner