Kongruenzabbildung - Geradenspiegelungen

Question

Ich habe eine Kongruenzabbildung (eine Drehung) vorliegen und habe die Abbildungspfeile (von z.B. A zu A') eingezeichnet. Nun sollen Geraden gefunden werden, mit denen "nach einer Verkettung der Geradenspiegelungen die abgebildete Bewegung entsteht".

Könnten damit die Mittelsenkrechten der Abbildungspfeile gemeint sein, deren Schnittpunkt das Drehzentrum ist?

Answer 1

Hallo,

Wenn Du eine Abbildung vorliegen hast, die mindestens zwei Punkte \(\{A,\, B, \dots \}\) durch eine Drehung auf \(\{A',\, B',\, \dots\}\) abbildet, dann ist der Schnittpunkt der Mittelsenkrechten der Strecken \(AA'\) und \(BB'\) der Drehpunkt \(D\).

Nun sollen Geraden gefunden werden, mit denen "nach einer Verkettung der Geradenspiegelungen die abgebildete Bewegung entsteht"

Du benötigst zwei Geraden, die durch \(D\) verlaufen und deren Winkel zueinander der halbe Drehwinkel (blau) ist. Eine einfache Lösung besteht darin, für die erste Spiegelung die Gerade \(a\) zu wählen,die durch \(D\) und \(A\) verläuft und als zweite die Mittelsenkrechte \(m\) der Strecke \(AA'\). Die beiden Spiegelungen sind dann \(s_a\) und \(s_m\).

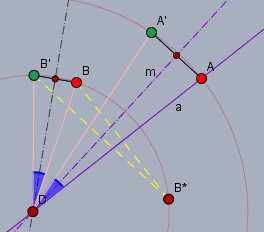
Man kann sich leicht überlegen, dass \(A\) durch \(s_m(s_a(A)) = A'\) auf \(A'\) abgebildet wird. Daselbe geschieht mit \(B\), wie im Bild oben durch die gelben gestrichelten Strecken zu sehen ist.

Eine Möglichkeit für das gesuchte Geradenpaar ist also \(a\) und \(m\) (beide lila).

Answer 2

Wenn du zwei Geraden g und h hast, die sich in einem Punkt S schneiden unter einem Winkel α schneiden, und du spiegelst einen beliebigen Punkt P an g zu P', und dann spiegelst du P' an h zu P'', dann entspricht die direkte Abbildung von P auf P'' einer Drehung von P um S um den Winkel  2α.

Mache dir das an einer entsprechenden Zeichnung klar.

Answer 3

Eine Drehung um den Wingel α und um den Punkt P ist ersetzbar durch eine Doppelspiegelung an zwei Geraden, die sich in P unter einem Winkel α/2 schneiden.