Bedingte Wahrscheinlichkeit (Wählerstimmen)

Question

Aufgabe:

Bei einer Bürgermeisterwahl erhielt von drei Kandidaten der Kandidat A 42,5% aller Stimmen. Bei der Analyse des Wahlergebnisses stellte sich heraus, dass Kandidat A von den über 50-jährigen, die 55,6% der Wähler ausmachen, mit 53% mehr als die Hälfte der Stimmen bekommen hat.

Wie viel Prozent der Wähler, die noch nicht 50 sind, haben einen anderen Kandidaten gewählt?

	A	Á
ü50	0,295	0,261	0,556
u50	0,13	0,314	0,444
	0,425	0,575	1

Die Vier-Felder-Tafel konnte ich erstellen.

Ich verstehe aber immer noch nicht den Unterschied zwischen P(u50 ∩ Á) und P_u50(Á). Das letzte wird ja anscheinend in der Aufgabe gesucht und wäre 70,65%. Aber warum nicht einfach die 31,4% aus der Tafel? Wo ist der Unterschied zwischen: Unter 50 und nicht A gewählt und und wie viel der Wähler die noch nicht 50 sind haben nicht A gewählt. Sorry, ich kann das zwar rechnen aber ich verstehe einfach den Unterschied überhaupt nicht.

Danke für eure Hilfe

Answer 1

Deine Vierfeldertafel ist richtig

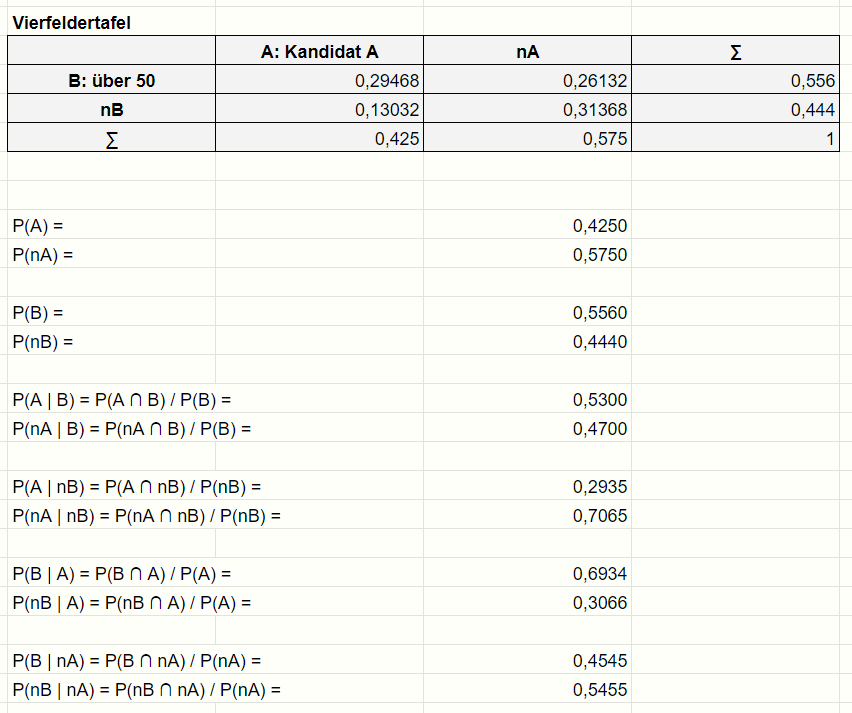
Wie viel Prozent der Wähler, die noch nicht 50 sind, haben einen anderen Kandidaten gewählt?

Hier ist eine bedingte Wahrscheinlichkeit gefragt. Bzw. um einen Anteil der Wähler, die noch nicht 50 sind.

Ich probiere dir hier mal die Bedeutung der Ausdrücke aufzuführen:

P(nA und nB) = 0.3137 wäre der Anteil an den gesamten Wählern die Kandidat A nicht gewählt haben und nicht über 50 Jahre alt sind. 31% aller Wähler haben nicht A gewählt und sind nicht über 50.

PnB(nA) = 0.7065 wäre der Anteil an denen die nicht über 50 Jahre sind die nicht Kandidat A gewählt haben. Also 71% der Wähler die nicht über 50 sind haben nicht Kandidat A gewählt.

PnA(nB) = 0.5455 wäre der Anteil an denen die nicht Kandidat A gewählt haben die nicht über 50 sind. Also 55% der Wähler die nicht Kandidat A gewählt haben sind nicht über 50.

Answer 2

Unter 50 und nicht A

Grundgesamtheit ist die Menge aller Wähler.

Wähler die noch nicht 50 sind

Grundgesamtheit ist die Menge der Wähler, die unter 50 sind.

Bedingte Wahrscheinlichkeit ist ein Mittel, aus Aussagen über die erste Grundgesamtheit Aussagen über die zweite Grundgesamtheit zu treffen.