$$K=\{(x,y)\in \mathbb{R}^2 : |x|+|y|>1 \, \land \, |x|+|y|<2\} \\ \, \, \, \, \,= \underbrace{\{(x,y)\in \mathbb{R}^2 : |x|+|y|>1\}}_{=:K_1}\cap \underbrace{\{(x,y)\in \mathbb{R}^2 : |x|+|y|<2\}}_{=:K_2}$$ Der Durschnitt endlich vieler offener Mengen ist offen. Wir zeigen also, dass \(K_1\) und \(K_2\) offen sind. Dafür definieren wir \(f: \mathbb{R}^2 \to \mathbb{R}, \, (x,y)\mapsto |x|+|y|\). Die Betragsfunktion ist auf ganz \(\mathbb{R}\) stetig, damit ist auch \(f\) auf ganz \(\mathbb{R}^2\) stetig.
\(K_1\) ist das Urbild der offenen Menge \(\{z\in \mathbb{R} : z>1\}\)
\(K_2\) ist das Urbild der offenen Menge \(\{z\in \mathbb{R} : z<2\}\)
Dass \(\mathbb{R}^2\backslash K \) nicht kompakt ist, liegt daran, dass diese Menge nicht beschränkt ist.
Addendum:
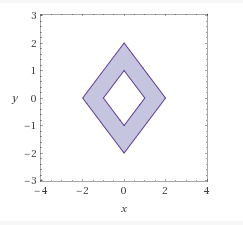
Die Menge \(K\) sieht übrigens so aus: