Berechne den Flächeninhalt der orangenen Fläche

Question

Aufgabe:

Berechne den Flächeninhalt der orangenen Fläche. a = 49 dm.

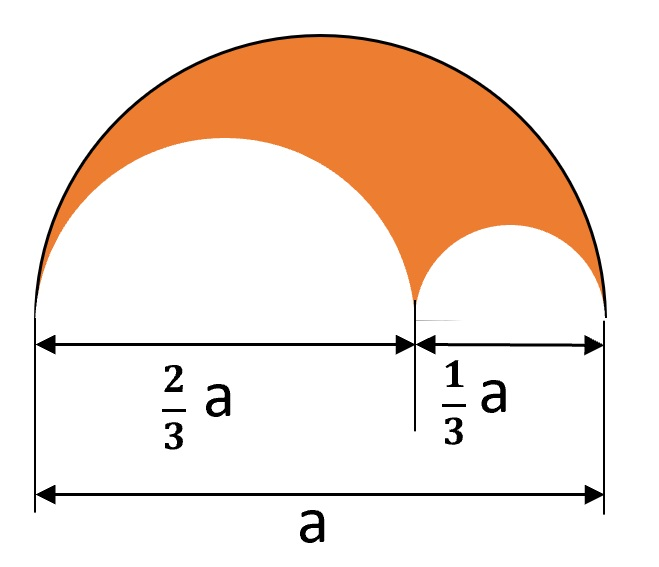
Problem/Ansatz:

ich habe 420,94 raus aber ich denke es ist falsch ich hoffe sie können mir helfen ........ ich weiß zwar das man die kreise einzel ausrechen muss und dann von dem großen abziehen muss aber ich denke ich habe es trodzdem falsch

Answer 1

a = 49 m ( durchmesser ) => r1 = 24.5 m
Mit 2/3 a : r = ( 2/3 * a ) / 2 => r2 = 16,33 m
Mit 1/3 a : r = ( 1/3 * a ) / 2 => r3 = 8.17 m

Von allen 3 Kreisen die Fläche berechnen
und dann 2+3 von 1 abziehen.
Die Berechnung gilt für Vollkreise.
Da es nur Halbkreise sind ist das Ergebnis
durch 2 zu teilen.

Comments

Glückwunsch zu den 100.000-Punkten!

---

Danke.
Ich lege auf die Punkte allerdings nicht so
viel wert.
Ich bin ja nur im Formum aus Gründen der
Kurzweil sowie zum Gehirnjoggen gegen
beginnende Demenz.

(* Scherzmodus an *)
der dänische Physiker hatte, wie viele seiner Landsleute, ein kleines Ferienhaus. Über der
Eingangstür hing ein Hufeisen als Glücksbringer.

Die ihn besuchenden Kollegen wunderten sich
über das Zeichen bei so einem rationalen
Menschen. Bohrs Kommentar :
" Man hätte ihm gesagt es würde auch wirken
auch wenn man nicht dran glaubt."
(* Scherzmodus aus *)

Answer 2

Du ziehst vom großen Halbkreis mit Durchmesser a die beiden kleineren Halbkreise mit Durchmesser 2/3*a und 1/3*a ab.

Answer 3

(24,5²-(49/3)²-(24,5/3)²)·π/2≈419,05 dm².

Nicht zu früh runden!

Comments

Nicht zu früh runden!

Falsch.

Gar nicht runden und ein genaues Ergebnis angeben.

Answer 4

A = 1/2·pi·(a/2)^2 - 1/2·pi·(2/3·a/2)^2 - 1/2·pi·(1/3·a/2)^2 = 1/18·pi·a^2

für a = 49 also

A = 1/18·pi·49^2 = 419.1 dm²

Damit ist deine Rechnung bis auf Rundungsdifferenzen wohl richtig.