Hallo,
einen wirklichen Ansatz habe ich nicht.
Dann mache Dir doch mal eine Zeichnung:
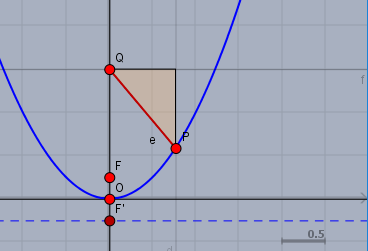
Die Funktion \(f(x)=x^2\) ist die Normalparabel (blau). Ein beliebiger Punkt auf der Parabel sei \(P\) mit den Koordinaten \(P(x|x^2)\). Um den Abstand zum einem Punkt \(Q(0|1,5)\) zu bestimmen, wähle den Satz des Pythagoras. Sei der Abstand \(e\) dann gilt:$$e = \sqrt{(x-0)^2 + (x^2 - 1,5)^2} = \sqrt{x^4 - 2x^2 + 2,25} \to \min$$Dieser Abstand \(e\) soll in Abhängigkeit von \(x\) minimiert werden. Es ist also eine klassische Optimierungsaufgabe.
Um Rechenarbeit zu sparen, kann man in diesem Fall auch das Quadrat \(e^2\) des Abstands minimieren. Dann gilt für die Extrempunkte$$\frac {\partial e^2}{\partial x} = 4x^3 - 4x \to 0 \\ x_1 = 0, \quad x_2 = 1, \quad x_3=-1 \\$$ Ein Blick in die Zeichnung hilft, um zu erkennen, dass es sich bei \(x_1=0\) um ein lokales Maximum handelt. Dann bleiben die Punkte$$P_2(1|1), \quad P_3(-1|1)$$ als die Punkte mit dem kürzesten Abstand zu \(Q\) übrig.
Geometrisch ist dies ebenso zu lösen.
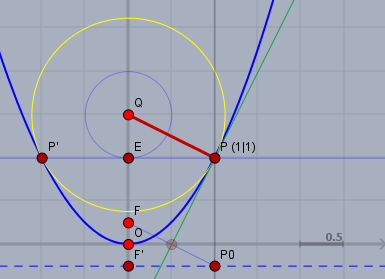
\(F\) ist der Brennpunkt der Parabel, \(F'\) seine Projektion auf die Leitgerade der Parabel. Das Viereck \(FP_0PQ\) ist ein Parallelogramm. Daraus folgt, dass \(|PP_0| = |QF|\) ist. Man schlägt also einen Kreis mit Radius \(|FF'|\) um \(Q\), der die Y-Achse in \(E\) schneidet und zeichnet eine Parallele zur X-Achse durch \(E\), die die Parabel in \(P\) und \(P'\) schneidet. Dies sind die gesuchten Punkte.
Der gelbe Kreis ist der kleinste Kreis um \(Q\), der die Parabel gerade noch berührt.
Im zweiten Fall, für \(Q(3|0)\), ist die Rechnung$$e = \sqrt{(x-3)^2 + (x^2 - 0)^2} = \sqrt{x^4 + x^2 - 6x + 9} \\ \frac {\partial e^2}{\partial x} = 4x^3 + 2x - 6 \to 0 $$Durch Raten findet man die Lösung \(x_1=1\), dann bleibt nach einer Polynomdivision durch \((x-1)\) $$4x^2+4x + 3 = 0$$übrig. Diese Gleichung hat aber keine weitere Lösung im reellen.