![image]()

![image]()
Vermeidung einer Funktion zu hohen Grades durch Ermittlung 2 Funktionen 4ten Grades
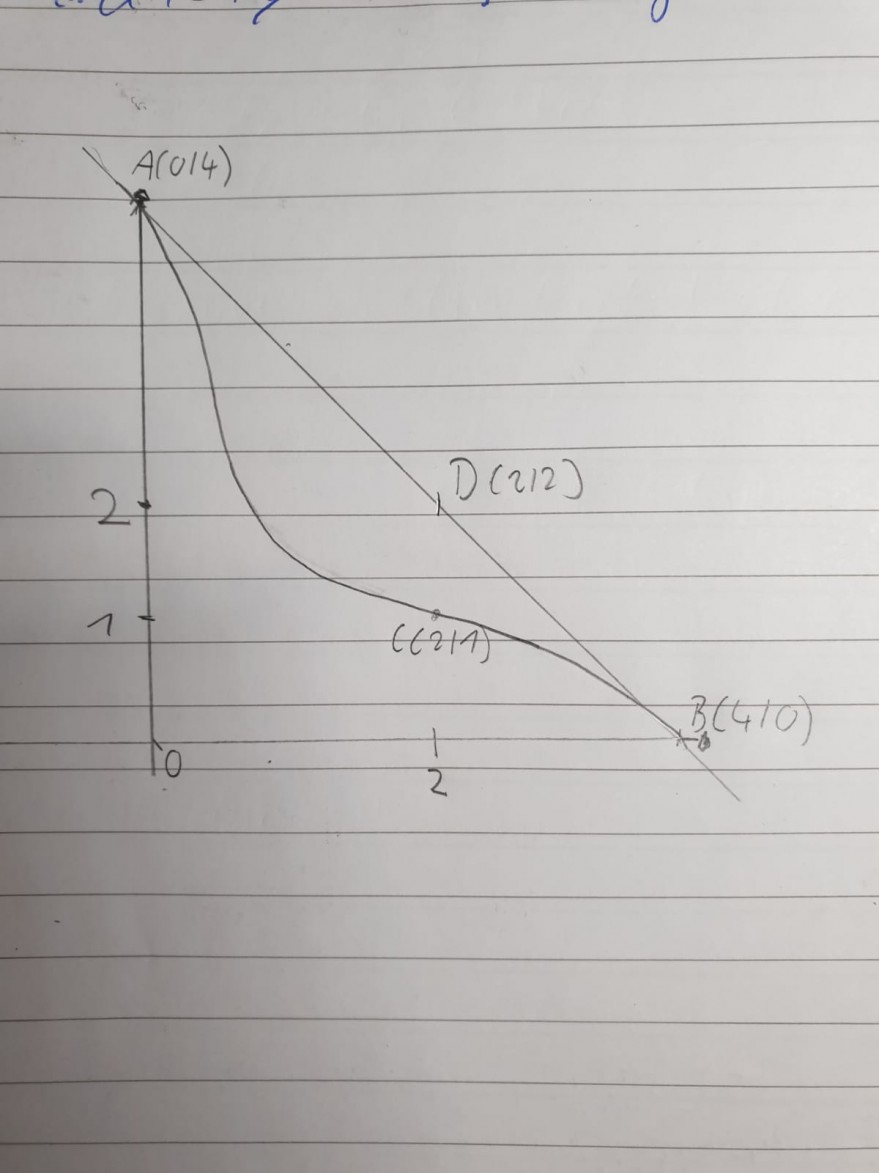
Aufgabe: Um Funktionen zu hohen Grades zu vermeiden, kann man 2 Funktionen 4ten Grades ermitteln, deren Graphen die Punkte A und C bzw. C und B miteinander verbinden. Es muss in C ein knickfreier und krümmungsruckfreier Übergang vorliegen. Dabei müssen die Funktionen auch knickfrei und krümmungsruckfrei in die jeweiligen Punkte A und B übergehen.
Problem/Ansatz:
Mein Bedingungen für die Funktion, die A und C miteinander verbinden: f(0)=4, f'(0)=-1, f''(0)=0, f(2)=1 und f''(2)=0
Bzw. Für die Funktion der Punkte B und C: f(4)=0, f'(4)=-1, f''(4)=0, f(2)=1 und f''(2)=0
Damit könnte ich 2 Funktionen 4ten Grades ermitteln aber dabei gibt es keinen knickfreien Übergang im Punk C wie gefordert war. Wie komme ich jetzt weiter? Ich darf ja keine weitere Bedingung hinzufügen, da ich sonst 2 Funktionen 5ten Grades ermittle.