Aufgabe:
Bestimmen Sie für folgende Funktionen jeweils alle p aus den nat zahlen mit f(h) = O(h^p) für
h --> 0
sin^2(x)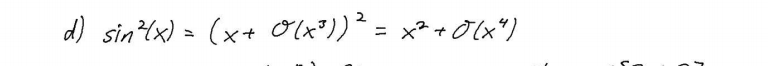
Text erkannt:
\( d) \sin ^{2}(x)=\left(x+\sigma\left(x^{3}\right)\right)^{2}=x^{2}+\sigma\left(x^{4}\right) \)
Wie kommt man auf diese Rechnung?