Wie findet man die Nullstellen von sin x heraus?

Question

Aufgabe:

Wie findet man die Nullstellen von sin x heraus?

Normalerweise findet man diese ja heraus, wenn man es mit 0 gleichsetzt. Wenn man dies hier machen würde, würde man 0 bekommen. Zwar ist dieses Resultat auch richtig, aber es gibt ja mehr Nullstellen. Wie finde ich diese nun heraus?

Answer 1

Wie findet man die Nullstellen von sin x heraus?

Man schaut auf dem Einheitskreis nach. Da ist sin(x) = 0 genau dann wenn x ein ganzzahliges Vielfaches von π ist.

Answer 2

SIN(x) = 0

Eine Lösung liefert die Umkehrfunktion

x = SIN^{-1}(0) = 0

Alle weiteren Lösungen erhältst du hier indem du vielfache von pi addiert

x = k·pi ; k ∈ ℤ

Man darf dafür wissen wie die Sinus-Funktion verläuft

Answer 3

Die Sinus-Funktion ist eine \(2\pi\)-periodische Funktion. Deshalb gibt es für alle \(x=\pi n\) mit \(n\) aus den ganzen Zahlen (für alle ganzzahligen Vielfachen von \(\pi\)) eine Nullstelle: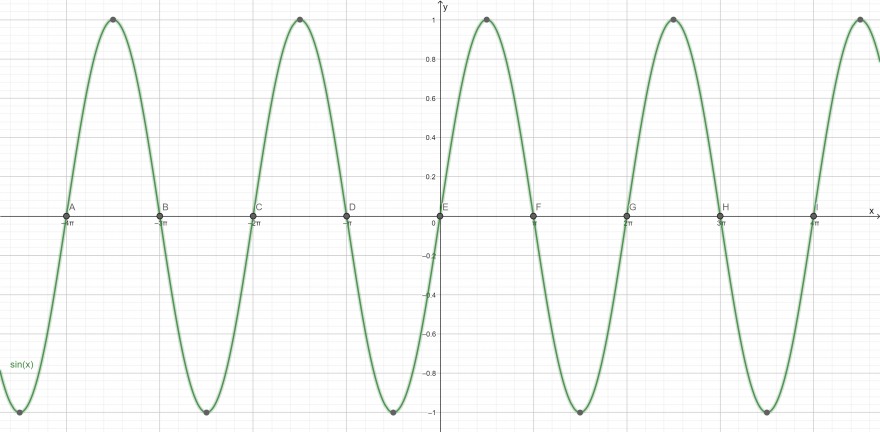

Hier in der Grafik siehst du die Nullstellen $$\begin{aligned}A&=-4\pi,& B&=-3\pi,& C&=-2\pi,& D&=-\pi,\\E&=0, & F&=\pi,& G&=2\pi,& H&=3\pi,& I&=4\pi\end{aligned}$$