Hallo Alina,
das ganze sollte man sich auf jeden Fall irgendwie aufzeichnen, um eine Vorstellung zu bekommen, was da passiert. Ich gehe davon aus, dass es sich um eine gerade Pyramide handelt, dann liegt ihre Spitze \(S\) stets oberhalb der Mitte der Grundfläche. Demnach ist $$S = \begin{pmatrix} t/2\\ t/2\\ t/8\end{pmatrix} =\frac 18 \begin{pmatrix} 4\\ 4\\ 1\end{pmatrix} \cdot t$$
Ich habe das hier mit Geoknecht3D dargestellt:
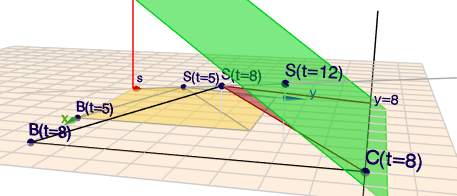
(klick auf das Bild und rotiere die Szene mit Maus, dann bekommst Du einen räumlichen Eindruck)
Die siehst die Ebene (grün) und eine Gerade durch den Ursprung, auf der die Punkte \(S(t)\) liegen. Die Punkte \(S(t=5)\), \(S(t=8)\) und \(S(t=12)\) habe ich eingezeichnet. Bei \(t=5\) hat die Pyramide (hellbraun) noch keinen Kontakt mit der Ebene. Bei \(t=12\) liegt die Spitze \(S(t=12)\) in der Ebene, aber auch viele andere Punkte der Pyramide.
Den ersten Kontakt einer steitig mit \(t\) wachsenden Pyramide haben die Punkte \(C\) und \(D\). Beide haben die gleiche Y-Koordinate \(t\) und liegen bei \(t=8\) in der Ebene. Da sie unabhängig von \(t\) immer die Z-Koordinate \(C_z = D_z = 0\) haben, müssen wir uns anschauen, wo die Punkte der Ebene bei \(z=0\) liegen:$$E: \quad 3y + 4z = 24 \\ z= 0 \implies y = \frac{24}3 = 8$$ Die Antwort auf die Frage
Für welches t haben die Pyramide und die Ebene gemeinsame Punkte?
lautet also: für alle \(t \ge 8\).
Gruß Werner