Goniometrie, Nullstellen: SIN(x) + SIN(2·x) = 0

Question

Text erkannt:

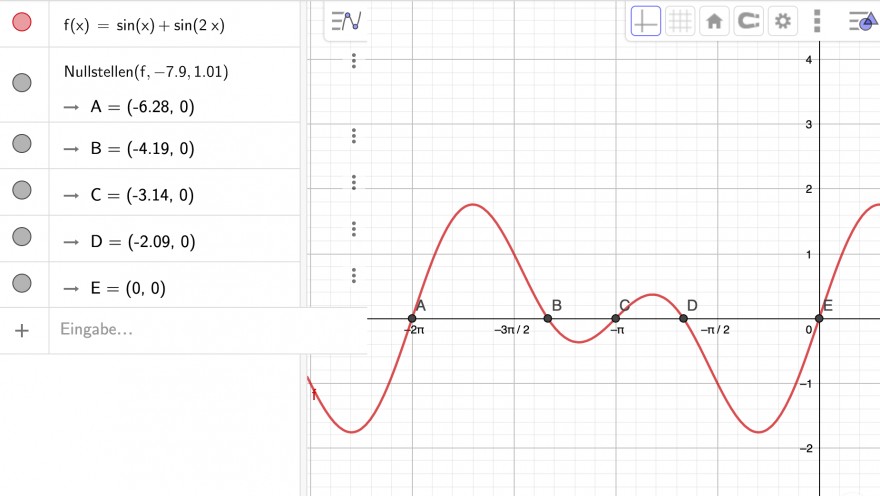
\( f(x)=\sin (x)+\sin (2 x) \)
Nullstellen \( (f,-7.9,1.01) \)
\( \rightarrow \mathrm{A}=(-6.28,0) \)
\( \rightarrow \mathrm{B}=(-4.19,0) \)
\( \rightarrow C=(-3.14,0) \)
\( \rightarrow \mathrm{D}=(-2.09,0) \)
\( \rightarrow \mathrm{E}=(0,0) \)
\( +\quad \) Eingabe...

ich habe die Gleichung f(x)=0 händisch gelöst und komme auf 2/3 Pi, was auch korrekt ist. Das gegbene Intervall geht aber von [-2pi;0). Gut dann mach ich mein Ergebnis eben negativ und bekomme -2/3 Pi, was ebenfalls stimmt. Mein Problem ist jetzt nur wie ich auf die restlichen Nullstellen komme ohne mir den Graphen hier anzeigen zu lassen etc. (ich muss das ganze ohne Hilfsmittel machen.) eine weitere Nullstelle würde man ja ganz simpel durch 2/3 Pi -2Pi berechnen aber auf die anderen zu kommen ist mir wirklich ein Rätsel.

Answer 1

SIN(x) + SIN(2·x) = 0
SIN(x) + 2·SIN(x)·COS(x) = 0
SIN(x)·(1 + 2·COS(x)) = 0

SIN(x) = 0 → x = k·pi ; k ∈ Z

1 + 2·COS(x) = 0 → ± 2/3·pi + k·2·pi ; k ∈ Z

Comments

oooh jetzt macht alles Sinn! Du hast mich schon so oft gerettet, danke!

Answer 2

Hallo

wie hast du es gelöst? sin(x)+2sin(x)*cos(x)=0 ist erstmal bei sin(x)=0 erfüllt, also für 0, -pi.-2pi und für 1+2*cos(x)=0 die hast du gefunden. Wahrscheinlich statt ausklammern durch sin(x) geteilt ohne dazu zu vermerken nur für sin(x)≠0

Gruß lul