Nullstellen bestimmen von f(x)= sin(2x) + cos(x - pi)

Question

Wie bestimme ich die Nullstellen der Funktion:

f(x) = sin(2x) + cos(x - π)

Die Nullstellen von der Lösung sind:

pi/2

3pi/2

pi/6

5pi/6

Answer 1

Vergleiche cos(x) mit cos(x-pi):

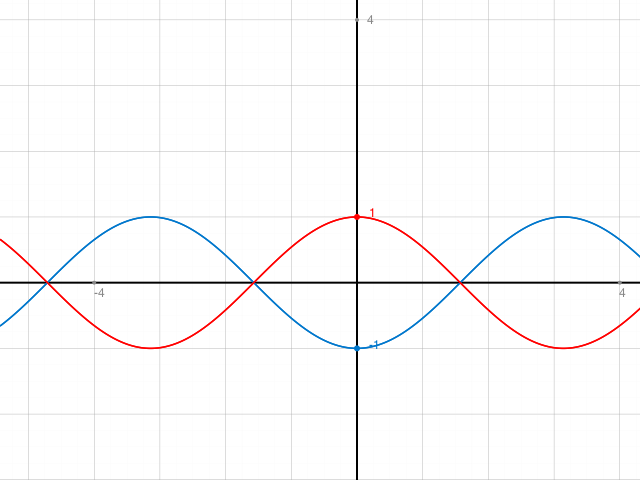
Daher die Gleichung neu:

sin(2x) + cos(x - pi) = 0

sin(2x) - cos (x) = 0            |Doppelwinkelformel

2sin(x) cos(x) - cos(x) = 0        |faktorisieren

cos(x) (2sin(x) - 1) = 0            |Faktoren Null setzen

1. cos(x) = 0     Cosinuskurve ansehen.----> x₁ = pi/2, x₂ = 3pi/2

2. 2sin(x) - 1 = 0

sin(x) = 0.5

x₃ = arcsin(0.5) = 30° = pi/6         

zudem x₄ = 180° - 30° = 5pi/6           |Sinuskurve ansehen

Das sind jetzt alle Lösungen von 0 bis 2pi.

 

Comments

könntest du vielleicht genau hinschreiben was du machst:

sin(2x) + cos(x - pi) = 0

sin(2x) - cos (x) = 0

2sin(x) cos(x) - cos(x) = 0        |faktorisieren         Wie kommt diese Zeile zu stande

cos(x) (2sin(x) - 1) = 0.

1. cos(x) = 0    →x1 = pi/2, x2 = 3pi/2

2. 2sin(x) - 1 = 0

sin(x) = 0.5

x3 = arcsin(0.5) = 30° = pi/6         zudem x4 = 180° - 30° = 5pi/6

Das sind jetzt alle Lösungen von 0 bis 2pi.

Answer 2

cos(x - pi) = -cos(x)

sin(2x) - cos(x) = 0

1) Nullstellen sind jene Stellen, wo sowohl sin(2x) als auch cos(x) Null sind. Das sind pi/2 und 3pi/2

2) Nullstellen sind auch jene Stellen, wo sowohl sin(2x) als auch cos(x) 1 sind. Solche gibt es hier nicht.

3) Zuletzt sind es die Stellen, wo sin(2x) = cos(x) ≠ 0 ist. Das wäre bei pi/6 und bei 5pi/6 der Fall.

Es empfiehlt sich auf jeden Fall, den Graphen der Funktion oder der Teile sin(2x) und cos(x) zu zeichnen.