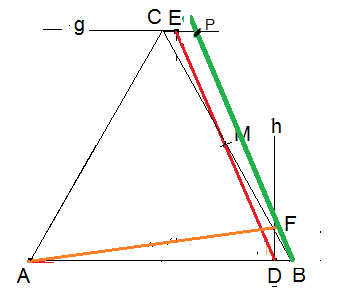
Ohne auf Details einzugehen: Die Dreiecke DBM und ECM sind kongruent, damit gilt DB = CE.
Eine Verschiebung der Strecke DE zum Punkt B erzeugt die grüne Strecke BP mit dem Punkt P,
für den jetzt PC = 2 CE gilt.
In dem kleinen Dreieck DBF gilt AUCH FB = 2 DB = 2 CE.
Damit sind die Dreiecke ABF und BPC kongruent (AB=BC, FB=PC und 60°=60°).
Wegen der Kongruenz der Dreiecke gilt AF=BP, und BP ist so lang wie ED.