Kurvendiskussion. Funktion ist ein Bruch f(x)=(x^2-3x+5) / (2x^2-4x+6). wie auflösen?

Question

 

gegeben ist die Funktion  f(x)=(x²-3x+5) / (2x²-4x+6). Jetzt muss ich alles einmal ausrechen. Wendepunkt, Nullstellen und die Symmetrie bestimmen. Ich meine es liegt keine Symmetrie vor, da die Exponenten unterschiedlich sind?

Wie löse ich diese Gleichung jetzt aber nach 0 auf?

Danke für die Hilfe!

Comments

Wie löse ich diese Gleichung jetzt aber nach 0 auf?

Du suchst die Nullstellen der Funktion?

Ein Quotient ist genau dann 0, wenn der Zähler 0 ist (und der Nenner nicht auch gerade noch 0 ist).

Löse also

x²-3x+5 = 0

nach x auf.

---

Als neue Frage gestellt. Setze es mal als Kommentar hier drunter:

 

Gegeben ist die Funktion f)x)=(X²-3x+5) / (2x²-4x+6)

Wie leite ich das jetzt richtig ab?

Meine Ableitung wäre (2x-3) / (4x-4), aber wenn ich das nach 0 auflöse, kommt der falsche Hochpunkt raus.. :/ Wo ist mein Fehler?

Answer 1

Ich habe die Aufgabe mal unter folgendem Link bearbeitet: https://docs.google.com/document/d/1KqQNTEMPCV9tNbuCB0t4eWEkpE9DJT-t2OsIGCDqwts/pub

Kurvendiskussion: f(x) = (x^2 - 3·x + 5)/(2·x^2 - 4·x + 6)

Funktion und Ableitungen

f(x) = (x^2 - 3·x + 5)/(2·x^2 - 4·x + 6) = 1/2 + (2 - x)/(2·x^2 - 4·x + 6)

f'(x) = (2·x^2 - 8·x + 2)/(2·x^2 - 4·x + 6)^2

f''(x) = (- 4·x^3 + 24·x^2 - 12·x - 16)/(2·x^2 - 4·x + 6)^3

Symmetrie

Keine erkennbare Symmetrie

 

Polstellen Nenner = 0

2·x^2 - 4·x + 6 = 0
Keine Polstellen

 

Asymptote

Horizontale Asymptote: y = 0.5

 

Y-Achsenabschnitt f(0)

f(0) = 5/6 = 0.833

 

Nullstellen f(x) = 0

(x^2 - 3·x + 5)/(2·x^2 - 4·x + 6) = 0

x^2 - 3·x + 5 = 0

Keine reellen Nullstellen

 

Extremstellen f'(x) = 0

(2·x^2 - 8·x + 2)/((2·x^2 - 4·x + 6)^2) = 0

2·x^2 - 8·x + 2 = 0

x = 2 - √3 ∨ x = x = 2 + √3

x = 0.268 ∨ x = 3.732

 

f(0.268) = √3/8 + 5/8 = 0.842 | Hochpunkt

f(3.732) = 5/8 - √3/8 = 0.408 | Tiefpunkt

 

Wendestellen f''(x) = 0

(- 4·x^3 + 24·x^2 - 12·x - 16)/(2·x^2 - 4·x + 6)^3 = 0

- 4·x^3 + 24·x^2 - 12·x - 16 = 0 | Hier hilft nur ein Näherungsferfahren

x = -0.584 ∨ x = 1.294 ∨ x = 5.290

 

f(-0.584) = 0.787

f(1.294) = 0.669

f(5.290) = 0.419

 

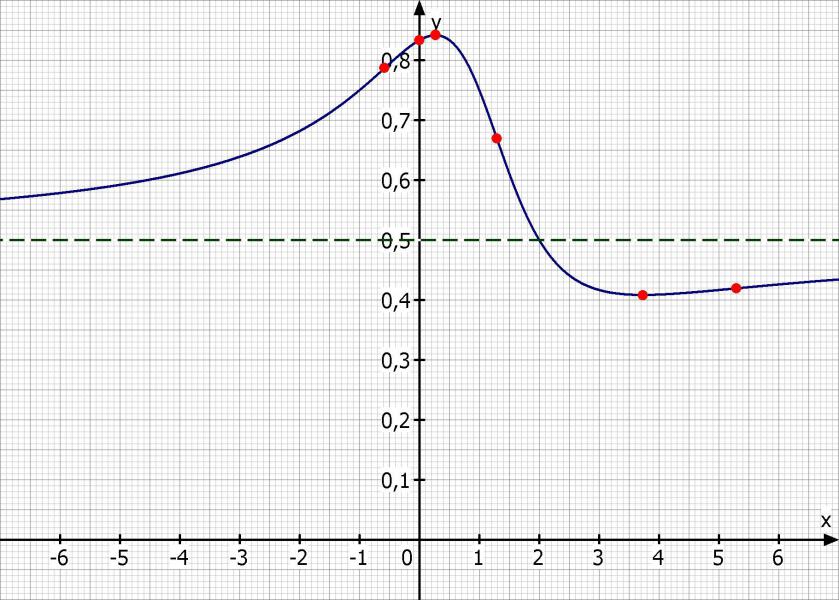
Skizze

Comments

@Der_Mathecoach: Habe die Daten aus deinem Dokument in der Antwort eingefügt. Für den Fall, dass Google Docs in den nächsten Jahren hops geht ;)

---

Mach mir nur keine Angst. Ich hoffe mal nicht das Google Docs irgendwann hops geht.

---

Du glaubst doch nicht, dass die Dotcom-Bubble im Jahr 2000 die letzte war... und bei Google's Reformchaos (wie Google Plus, Zusammenführung aller Dienste etc.) weiß man nie so recht, was als nächstes kommt.

Wer hierüber diskutieren möchte → ab in den Chat :)