Funktion aufstellen Fallunterschied

Question

Aufgabe:

Erstellen Sie eine Funktion zu folgenden Aufgabe:

Wenn x<0 ist, dann soll x+1 gerechnet werden

Wenn x>0 ist, dann soll x-2 gerechnet werden

Answer 1

Hallo,

du kannst einfach eine Funktion basteln, die die Fallunterscheidung enthält: $$f(x)=\begin{cases}x+1 & \text{falls } x<0 \\ x-2 & \text{falls } x>0\end{cases}$$ Immer wenn \(x<0\) ist, wird \(x+1\) gerechnet und sonst \(x-2\).

Die Funktion sieht dann wie folgt aus: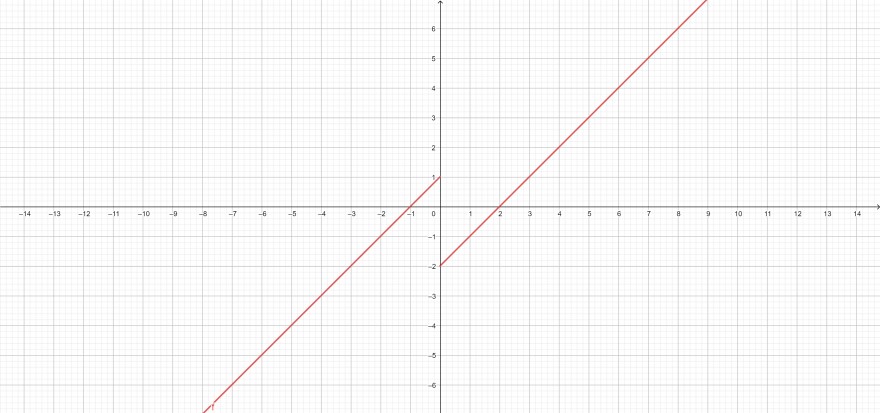

Weil die Funktion für \(x=0\) nicht definiert ist, hat sie dort einen "Sprung".

Answer 2

Ohne Fallunterscheidung:

f(x)=x-0,5 -1,5*\( \frac{|x|}{x} \)

Comments

Nur wenn \(x\neq 0\) ist. Ich würde es zur Sicherheit noch angeben.

---

Dass x≠0 ist, ergibt sich zwangsläufig. Meine angegebene Funktion liefert genau die vorgegebenen Werte und wegen der eingebauten undefinierten Stelle auch genau den erforderlichen Definitionsbereich.

---

Ich verstehe, wie du das meinst. Meine Idee mit der Angabe \(x\neq 0\) wäre also nur vonnöten, wenn der Bruch fehlen würde.

---

Könntest du mir schreiben, wie du auf solche Funktionen kommst? Also ich verstehe die Funktion, aber ich weiß nicht ob ich so eine bei einer anderen Aufgabe bilden könnte