Rutschbahn: Bestimmen Sie das maximale Gefälle auf der Rutsche und das durchschnittliche Gefälle

Question

Aufgabe:

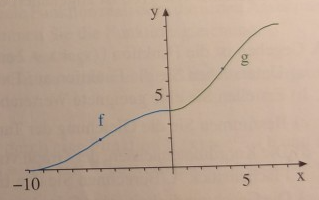
Eine Rutschbahn im Adventure-Park wird im Querschnitt dargestellt von zwei sinusförmigen Teilen, jeweils auf der Länge einer halben Periode.

a) Entwickeln Sie zwei trigonometrische Funktionen $\mathrm{f}$ (für $-10 \leq \mathrm{x} \leq 0$ ) und $g$ (für $0 \leq x \leq 8$ ), die zusammen das Profil der Rutsche beschreiben.

b) Bestimmen Sie das maximale Gefälle auf der Rutsche und das durchschnittliche Gefälle sowie die zuge-
hörigen Neigungswinkel.

c) Eine Firma möchte eine Werbefläche von mindestens $60 \mathrm{m}^{2}$ mieten. Würde eine seitliche Verkleidung der Rutsche dieser Anforderung genügen?

Problem/Ansatz:

Die a) konnte ich lösen.

F(x)=2sin(pi/10(x+5))+2

G(x)=3sin(pi/8(x-4))+7

Muss ich bei der b) den WP berechnen?

Die c) hänge ich komplett.

Answer 1

a) ist richtig

b) Du kennst bereits den Wendepunkt der beiden Funktionsteile. (-5 | 2) sowie (4 | 7). Damit hast du doch die Sinusfunktion aufgestellt. Du kannst aber auch den Wendepunkt bestimmen.

Bei c) sollst du die Fläche zwischen dem Graphen und der x-Achse ausrechnen. Hier möchte man also ein wenig Integralrechnung sehen. Du kannst aber auch hier durch geschicktes Aufteilen der Fläche die Integralrechnung umgehen.

Comments

Kansst du mir helfen den Neigungswinkel zu berechnen. Das fehlt mir noch.

---

b)
1 · pi/8 · 3/1 = 3/8·pi = 1.178

g'(x) = 3·pi/8·COS(pi/8·(x - 4))
g'(x) = 3·pi/8·COS(pi/8·(4 - 4)) = 3/8·pi = 1.178
α1 = ARCTAN(1.178) = 49.67°

10/18 = 5/9 = 0.5556
α2 = ARCTAN(5/9) = 29.05°

Answer 2

Hallo

ja, bei sin Funktion ist die maximale Steigung im Wendepunkt, ( max von f' bei f''=0) (allerdings sollte man den Wendepunkt von sin bei 1/2 Periode kennen und nicht berechnen müssen)

Aber ausrechnen Schadt ja nichts.

Gruß  lul