Aufgabe
f(x)=3/5-4x
Problem/Ansatz
Wie komm ich auf die Ableitung mithilfe der h-Methode?
Sieht die Gleichung so aus?
f(x)=35−4xf(x)=\frac{3}{5}-4xf(x)=53−4x
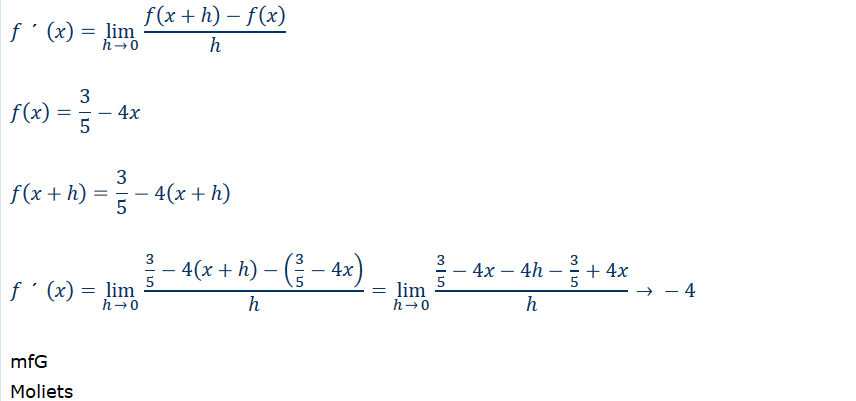
Text erkannt:
f′(x)=limh→0f(x+h)−f(x)h f^{\prime}(x)=\lim \limits_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} f′(x)=h→0limhf(x+h)−f(x)f(x)=35−4x f(x)=\frac{3}{5}-4 x f(x)=53−4xf(x+h)=35−4(x+h) f(x+h)=\frac{3}{5}-4(x+h) f(x+h)=53−4(x+h)f′(x)=limh→035−4(x+h)−(35−4x)h=limh→035−4x−4h−35+4xh→−4 f^{\prime}(x)=\lim \limits_{h \rightarrow 0} \frac{\frac{3}{5}-4(x+h)-\left(\frac{3}{5}-4 x\right)}{h}=\lim \limits_{h \rightarrow 0} \frac{\frac{3}{5}-4 x-4 h-\frac{3}{5}+4 x}{h} \rightarrow-4 f′(x)=h→0limh53−4(x+h)−(53−4x)=h→0limh53−4x−4h−53+4x→−4mfG \mathrm{mfG} mfGMoliets
Ein anderes Problem?
Willkommen bei der Mathelounge! Stell deine Frage einfach und kostenlos
