Wie geht man da vor und wie sind die Ausgangsgleichungen?

Question

Aufgabe:

gegeben: f(x)=2*x²  und g(x)=1/3*x³-4*x Schnittstellen bei x1=0 und x2=-1,5826..

f´(x)=4*x → f´(0)=m1=0  und f´(-1,58..)=m1=-6,3304

g´(x)=x²-4 → g´(0)=m3=-4 und g´(-1,58..)=m4=-1,495

Nun soll eine Funktion h(x)=... ermittelt werden,die beide Funktionen f(x) und g(x) "krümmungsruckfrei" verbindet.

Wie geht man da vor und wie sind die Ausgangsgleichungen ?

Problem/Ansatz:

~plot~2*x^2;1/3*x^3-4*x;[[-8|8|-10|10]];x=0;x=-1,5826~plot~

Comments

Nun soll eine Funktion h(x)=... ermittelt werden,die beide Funktionen f(x) und g(x) "krümmungsruckfrei" verbindet.

Zwischen welchen beiden Stellen?

Abgesehen davon ergeben sich 4 Forderungen:

Übereinstimmung der Funktionswerte an beiden Stellen

Übereinstimmung der Anstiege an beiden Stellen.

Damit genügt eine Funktion dritten Grades, deren allgemeine Form du in nahezu jeder privat im Buchhandel erwerbbaren Formelsammlung findest.

---

hallo

krümmungsrockfrei heisst auch noch h''(x^)=f''(x1) bzw. h''(x2)=g''(x2)

Gruß lul

---

abakus, müssen bei krümmungsruckfrei nicht auch die 2. Ableitungen an den Stellen übereinstimmen?

---

ein Typ hat ausgerechnet,dass

h(x)=-2,5*x^5+25,5625*x^4-96*x³+161,625*x²-121*x+34,3125  die gesuchte Funktion sein soll.

Wieso,weshalb,warum und wie die Ausgangsformeln sein sollen,keine Ahnung.

---

Welches sind denn die beiden Stellen, an denen die Übergänge gebildet werden sollen, x1 und x2?

---

hallo

wir hatten dir doch gesagt, dass die funktion 6 Bedingungen erfüllen muss, die musst du halt aufschreiben und alle in die allgemeine Gleichung für ein Polynom 5zen Grades einsetzen und dann ein Gleichungssystem lösen. Ohne einige Schreibarbeit geht das nicht.

Warum sagst du nicht, was du an den antworten nicht verstehst oder damit kannst. Oder frag den "Typ" um ne Nachhilfestunde !

die Lösung sieht allerdings nicht sehr gut aus.

lul

Answer 1

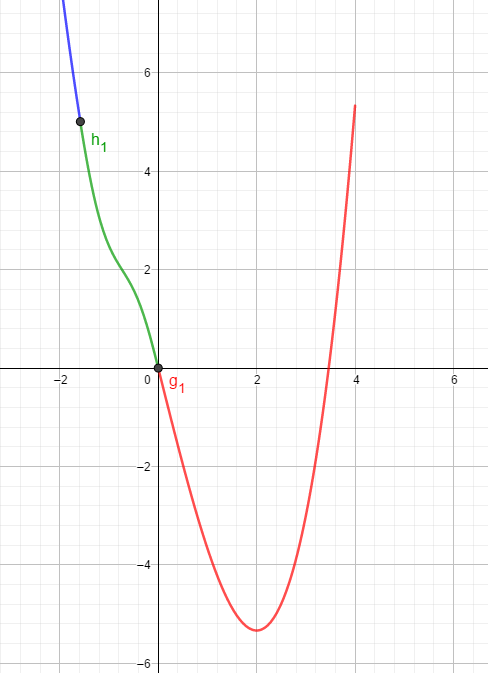
Hallo,

\(h(x)=ax^5+bx^4+cx^3+dx^2+ex+f\\h'(x)=5ax^4+4bx^3+3cx^2+2dx+e\\h''(x)=20ax^3+12bx^2+6cx+2d\)

Du stellst folgende Bedingungen auf:

\(\text{1. sprungfrei: }f(-1,58)=h(-1,58)\Rightarrow\\5,01=-9,85a+6,23b-3,94c+2,5d-1,58e+f\\\text{2. sprungfrei: }g(0)=h(0)\Rightarrow f=0\\[20pt]\text{1. knickfrei: }f'(-1,58)=h'(-1,58)\Rightarrow\\ -6,32=31,16a-15,78b+7,49c-3,16d+e\\ \text{2. knickfrei: }g'(0)=h'(0)\Rightarrow-4=e\\[20pt] \text{1. krümmungsruckfrei: }f''(-1,58)=h''(-1,58)\Rightarrow\\ 4=-78,89a+29,96b-9,48c+2d\\ \text{2. krümmungsruckfrei: }g''(0)=h''(0)\Rightarrow d=0\)

Streiche d und f, ersetze e durch -4. Dann bleiben noch drei Gleichungen mit drei Unbekannten.

Mein Ergebnis: \(h(x)=1,41x^5+5,67x^4+5,78x^3-4x\)

Aber rechne zur Sicherheit nochmal nach, denn ich kann mich leicht irgendwo verrechnet oder vertippt haben. Hauptsache, du hast die Vorgehensweise verstanden.

Gruß, Silvia