Berechnen Sie die Tangente t, die an Funktion f gelegt wird.

Question

Aufgabe:

f(x) = (x-2)e^x

Punkt A (1,5/1,5)

Berechnen Sie die Tangente t, die an Funktion f gelegt wird.

Problem/Ansatz:

Ich weiß nicht wie ich das rechnen soll.

Comments

Da passt was nicht. Der Punkt \(A(1,5|1,5)\) liegt nicht auf dem Graphen der Funktion, denn:$$f(1,5)\ne1,5$$

---

Das ist das Problem, gesucht ist die Tangente, die durch diesen Punkt geht. An jeder Stelle der Funktion gibt es eine Tangente,und eine dieser Geraden, geht durch A(1,5;1,5)

---

Seltsam nur, dass es keine Lösung für $$t(1.5)=f'(a)(1.5-a)+f(a)=1.5$$ gibt.

---

An jeder Stelle der Funktion gibt es eine Tangente, und eine dieser Geraden, geht durch A(1,5; 1,5)

Ist das wirklich so? Hast du das geprüft?

---

Es scheint tatsächlich keine Tangente hier zu geben:

---

Wenn es keine gibt, umso besser.

Answer 1

Das soll sicher A(1.5 | f(1.5)) lauten

Funktion und Ableitung

f(x) = e^x·(x - 2)
f'(x) = e^x·(x - 1)

a = 1.5
f(a) = - e^(3/2)/2
f'(a) = e^(3/2)/2

Tangente

t(x) = f'(a)·(x - a) + f(a)

t(x) = e^(3/2)/2·(x - 1.5) - e^(3/2)/2 = e^(3/2)·(2·x - 5)/4 = 0.25·e^1.5·(2·x - 5) = 2.240844535·x - 5.602111337

Answer 2

Hallo,

berechne die y-Koordinate des Punktes, indem du 1,5 für x in die Ausgangsgleichung einsetzt.

[spoiler]

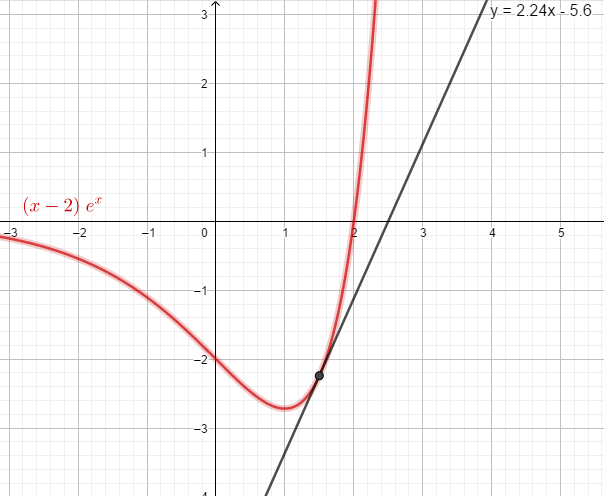
$$f(x)=(x-2)\cdot e^x\\ f(1,5)=(1,5-2)\cdot e^{1,5}=-2,24\\P(1,25|-2,24)$$

[/spoiler]

Berechne die Ableitung an der Stelle x = 1,5

[spoiler]

$$f'(x)=x\cdot e^x-e^x\\f'(1,5)=1,5\cdot e^{1,5}-e^{1,5}=2,24$$

[/spoiler]

Nun hast du die Steigung m der Tangentengleichung y = mx + b

Um b zu bestimmen, setzt du die Koordinaten des Punktes und die Steigung in diese Gleichung ein und löst nach b auf.

[spoiler]

$$y=2,24x+b\\ -2,24=2,24\cdot 1,5 + b\\ b = -\frac{28}{5}=-5,6\\[20pt] \text{Tangentengleichung:}\\y=2,24x-5,6$$

[/spoiler]

Gruß, Silvia