„Mathematik ist schön“ (https://www.amazon.de/dp/366259059X) ist der Titel eines Buches von Heinz Klaus Strick, dem viel daran liegt, im Mathematikunterricht die Schönheit der Mathematik für Schülerinnen und Schüler erkennbar zu machen.
Im Vorwort zur zweiten Auflage schreibt Strick:
Nicht jeder denkt, wenn von Mathematik die Rede ist, unbedingt an etwas, an dem man sich erfreuen kann. Dabei hat die Mathematik viele spannende und durchaus auch ästhetisch ansprechende Aspekte zu bieten. In diesem Buch versuche ich einige dieser schönen Seiten der Mathematik aufzuzeigen.
Im ersten Kapitel schlägt Strick vor, sich mit regelmäßigen Sternfiguren zu beschäftigen.
Dieses Thema ist auch Gegenstand der „Denkaufgaben aus der elementaren Geometrie“, welche man unter
https://www.mathelounge.de/529063/denkaufgaben-aus-der-elementaren-geometrie findet. Hier werden die regelmäßigen Sterne mit dem Begriff „n,k-Sterne“ bezeichnet, der die regelmäßigen n-Ecke als Sonderfall (k=1) mit einschließt.
Ein regelmäßiges n-Eck ist ein geschlossener konvexer Streckenzug aus n gleichlangen Strecken mit n gleichgroßen Innenwinkeln. Ein n,k-Stern entsteht, wenn man n Punkte regelmäßig auf einem Kreis verteilt und die Punkte von A0 bis An-1 im Kreise herum benennt. Dann ergeben alle Verbindungsstrecken AiAi+k (i=0, 1, 2, 3, ...) einen n,k-Stern (für i+k>n ist n zu subtrahieren).
Die Abbildungen zeigen einen 8,2-Stern (unten) und einen 5,2-Stern, der auch unter dem Namen ‚Pentagramm‘ bekannt ist (oben).
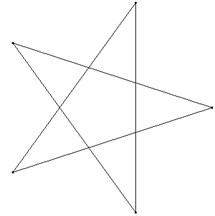
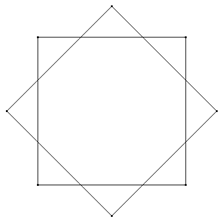
Zum Einstieg in die Thematik sollten insbesondere jüngere Schülerinnen und Schüler einige Sterne mit Geodreieck und Zirkel zeichnen. Das regelmäßige Anordnen von n Punkten auf einem Kreis ist eine gute Übung zum Antragen von zuvor berechneten Winkeln an den Radius eines Kreises.
Im weiteren Verlauf des Unterrichts kann das Zeichnen der regelmäßigen Sterne und n-Ecke von einem Computer-Algebra-System (CAS) oder von einem dynamischen Geometrie-System (DGS) übernommen werden. Dies gelingt insbesondere dann, wenn Punkte auf dem Einheitskreis als Zahlenpaare [cos(a), sin(a)] interpretiert werden können.
Ein regelmäßiges Achteck (oder hier: ein 8,1-Stern) wird dargestellt durch die Punkte [cos(2πk/8), sin(2πk/8)] mit k=0,…,8, die in dieser Reihenfolge von einem Polygonzug durchlaufen werden. Um einen 8,3-Stern zu zeichnen, muss der Polygonzug immer zwei Punkte überspringen und k muss die Zahlen 0, 3, 6, 1, 4, 7, 2, 5, 0 durchlaufen. In der Computeralgebra erhält man diese Zahlenfolge als mod(3m,8) für m=0,…,8. Die Punkte heißen dann in der Reihenfolge [cos(π/4· mod(3m,8)), sin(π/4·mod(3m,8))] für m=0,…,8.
Am Rande sei erwähnt, dass ein 8,3-Stern die Darstellung einer arithmetischen Folge mit der konstanten Differenz d=3 auf einem aufgewickelten Zahlenstrahl mit 8 Einheiten pro Wicklung ist. Siehe: https://www.mathelounge.de/683351/folgendarstellung-auf-einem-aufgewickelten-zahlenstrahl
Schon früh stellen Schülerinnen und Schüler fest, dass es Sterne gibt, die nur aus einem Streckenzug bestehen und die sich gewissermaßen ‚ohne abzusetzen‘ vollständig zeichnen lassen und solche, bei denen das nicht der Fall ist. Als Beispiele haben wir den 8,2-Stern und den 5,2-Stern kennengelernt. Die mathematische Beschreibung dieses Unterschiedes führt unmittelbar zum Begriff des größten gemeinsamen Teilers.
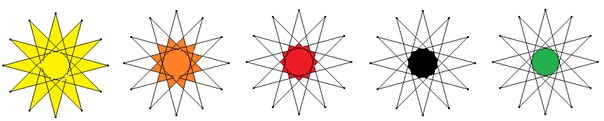
Weiterhin fällt auf, dass für jedes k∈ℕ der 2k,k-Stern aus k Strecken besteht, also wieder ein Sonderfall eines Sterns ist. Abgesehen von den Sonderfällen ist auch die Frage nach der Anzahl verschiedener n,k-Sterne bei gegebenem n interessant. Beispielsweise werden (außer k=6) alle verschiedenen 12,k-Sterne im 12,5-Stern sichtbar.
Im 3. Kapitel schlägt Strick ein Spiel vor:
Der beginnende Spieler zeichnet ein beliebiges Rechteck auf ein Blatt Papier mit Rechenkästchen. Dabei liegen die Rechteckseiten auf den Linien des Kästchenrasters. Der zweite Spieler trägt dann ein möglichst großes Quadrat links und oben bündig in dieses Rechteck ein, sodass ein Rechteck übrig bleibt. Dann ist wieder der erste Spieler an der Reihe, der in das verbliebene Rest-Rechteck ein möglichst großes Quadrat einzeichnet usw. Das Spiel endet, wenn das Ausgangsdreieck mit Quadraten ausgefüllt ist. Gewonnen hat derjenige Spieler, der das letzte Quadrat einzeichnen konnte.
Nehmen wir an, der erste Spieler zeichnet ein 8×3-Rechteck. Die vom zweiten Spieler eingezeichneten Quadrate seien rot, die vom ersten gelb unterlegt:
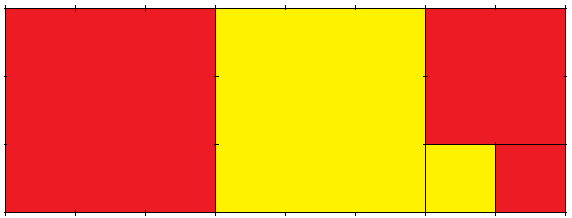
Überlegungen zur Gewinnstrategie zeigen, dass bereits der erste Spieler über Sieg oder Niederlage entscheiden kann, wenn er die Kettenbruchdarstellung von \( \frac{8}{3} \) kennt: 2+1/(1+1/2) oder in Kurzform [2, 1, 2]. Wenn die Summe 2+1+2 ungerade ist, gewinnt der erste Spieler.
Zwischen der Gewinnstrategie dieses Spiels und der Anzahl der geschlossenen Polygonzüge beim Zeichnen eines regelmäßigen Sterns besteht ein Zusammenhang, dessen Bindeglied der Euklidische Algorithmus ist.