Hallo,
Welche Formel muss ich bei der Projektion anwenden ..
Die Frage nach der Formel ist immer die falsche Frage. Die Formel nützt Dir nichts, wenn Du nicht weißt, was Du damit rechnest, selbst wenn am Ende das richtige Ergebnis raus kommt.
... und wie versteht man die zweite Teilaufgabe?
das zeigt, dass Du die Aufgabenstellung nicht verstanden hast; es gibt keinen zweiten Teil. \(x_{\parallel}\) ist die Projektion von \(x\) auf etwas - also hier wohl auf \(y\). Ist \(x_{\parallel}\) berechnet, so ist auch die Zerlegung bekannt.
Folgendes Bild:
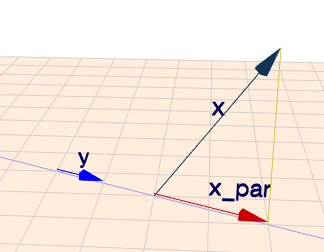
Die Projektion des Vektor \(x\) auf \(y\) ist das was übrig bleibt, wenn man alle Punkte, aus denen der Vektor \(x\) besteht, senkrecht auf die Gerade (hellblau) fallen lässt, die durch den Vektor \(y\) (blau) definiert ist. Hier ist das der rote Vektor \(x_{\parallel}\) alias \(x_{\text{par}}\).
Das ganze noch mal in 2D:
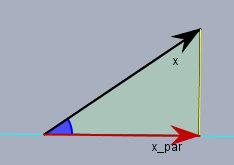
Die Länge von \(x_{\parallel}\) ist \(|x_{\parallel}| = |x| \cdot \cos \varphi\). Wobei \(\varphi\) (blau) der Winkel zwischen dem Vektor \(x\) und der Bezugsrichtung (hellblau) ist. Jetzt weiß Du vielleicht, dass das Skalarprodukt zweier Vektoren \(a\) und \(b\) wie folgt definiert ist $$a^T \cdot b = |a| \cdot |b| \cdot \cos \varphi$$ \(\varphi\) ist wieder der Winkel zwischen den beiden Vektoren. Hat nun der erste die Länge 1 und der zweite ist \(x\), dann ist $$n^T \cdot x = |x| \cdot \cos \varphi, \quad |n| = 1$$Und das ist nichts anderes als die Länge der Projektion. Man braucht also nur den Vektor \(y\) zu normieren und schon kann man die Länge von \(x_{\parallel}\) aus dem Skalarprodukt berechnen$$|x_{\parallel}| = \left( \frac{y}{|y|}\right)^T \cdot x$$Das ist aber nur ein Skalar. Um daraus einen Vektor zu machen, der parallel zu \(y\) läuft, also in Richtung \(y\) zeigt, multipliziert man diesen Wert noch mit dem Einheitsvektor von \(y\):$$x_{\parallel} = \left( \left( \frac{y}{|y|}\right)^T \cdot x \right) \cdot \frac{y}{|y|} = \frac{y^T x}{|y|^2} \cdot y = \frac{y^T x}{y^T y} \cdot y $$Und die nummerische Berechnung kannst Du ruhig einem Rechenknecht überlassen, z.B. einem Tabellenkalkulationsprogramm:

In den Zellen B8 und C8 steht das Ergebnis der Matrizenmultiplikation \(y^T \cdot (x,y)\). Teilt man die beiden Zahlen durcheinander, so erhält man den Faktor \(-2/7\), mit dem \(y\) multipliziert werden muss, um \(x_{\parallel}\) zu erhalten. Und \(x_{\perp}\) ist dann schlicht \(x_{\perp} = x - x_{\parallel}\).