Hallo Carla,
Willkomen in der Mathelounge!
Berechne die Projektion lambda*v des Vektors w=[1,1,-1] auf Lin{v},
Wenn \(\lambda v\) die Projektion von \(w\) auf \(v\) sein soll, dann muss \(w-\lambda v\) orthogonal zu \(v\) stehen. Das Bild zeigt den Differenzvektor \(w-\lambda v\) in hellblau für \(a=-0,5\)
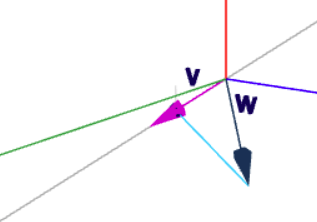
D.h. das Skalarprodukt dieser beiden Vektoren ist 0. Daraus folgt$$\begin{aligned} 0&=\left<(w-\lambda v),\, v \right> \\ 0 &= \left<w,\,v\right> - \lambda\left< v,\, v \right> \\ \implies \lambda &= \frac{\left<w,\,v\right>}{\left< v,\, v \right>}\\ \lambda &= \frac{1+a-a}{1+a^2+a^2}\\ \lambda&= \frac{1}{1+2a^2} \end{aligned}$$Also ist \(\lambda v\)$$\lambda v = \begin{pmatrix}x\\ y\\ z\end{pmatrix} = \frac{1}{1+2a^2} \begin{pmatrix} 1\\a\\a \end{pmatrix}$$Gruß Werner