Text erkannt:
tonlesatz
n denen die Funktion \( f \) streng mono
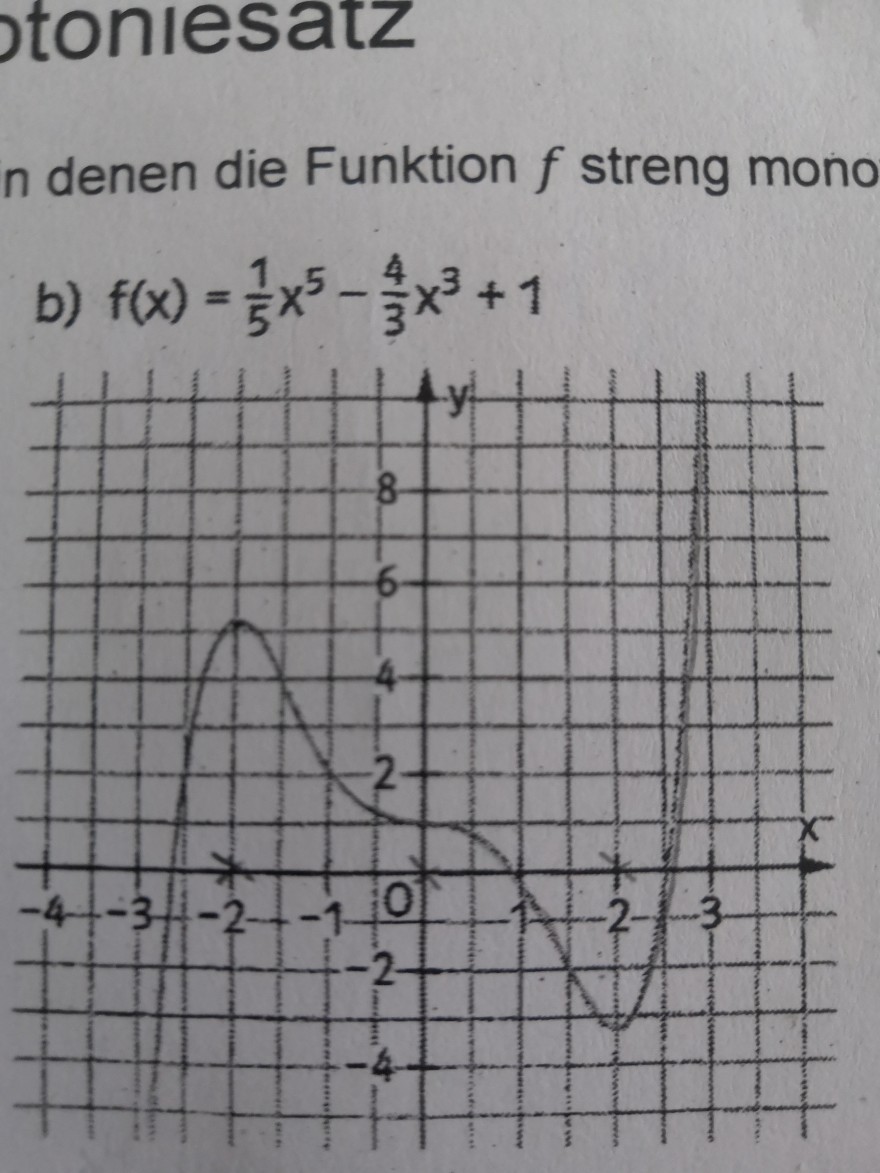
\( f(x)=\frac{1}{5} x^{5}-\frac{4}{3} x^{3}+1 \)
Heyy, ich hab ein kleines Problem mit der Monotonie und fand das schwierig zu erklären ohne dass man den Graphen vor sich hat (deshalb das Bild). Hoffe, dass das in Ordnung ist!
Aufgabe:
Gib möglichst große Intervalle an, in denen die Funktion von f streng monoton wachsend bzw. fallend ist
Problem/Ansatz:
In det Aufgabe heißt es ja eigentlich nur mit streng monoton, aber an der Stelle x=0 befindet sich glaube ich eine Sattelstelle (Ableitung dort ergibt 0) und es gibt keinen Vorzeichenwechsel.
Heißt das, dass der Graph an dieser Stelle nur monoton fallend ist und wenn ja, sagt man dann im Intervall (-2;2) oder in den Intervallen (-2;0) und (0;2).
Ich habe mit Sattelstellen das Problem, dass ich da nicht weiß, wann es nur monoton steigend und wann streng monoton steigend ist.
Wäre mega, wenn mir jemand helfen könnte!