Extremwertaufgabe (Glasscheibe aus Glasrest)

Question

 

habt ihr weitere Lösungsvorschläge, Hinweise, Ideen  für die Extremwertaufgabe?

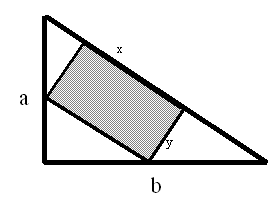
Das Rechteck liegt in dem Dreieck zunächst waagerecht, also quer drin. Später (in Aufgabe 6) wird es dann gedreht.

Ein Glaser will aus einem dreieckig rechtwinkligen Glasrest

(mit den Kathetenlängen a = 6 LE  bzw.  b = 4 LE) eine möglichst große rechteckige Scheibe ausschneiden.

Der Flächeninhalt des Rechtecks soll möglichst groß werden.

1  Stelle für die Fläche der rechteckigen Glasscheibe die Flächenfunktion in Abhängigkeit von den Seiten  a  und  b  auf.              Zielfunktion mit 2 Variablen                       x  *  y  =  ?   (?, weil noch nicht bekannt)

2  Gib anhand der Grenzlagen der rechteckigen Glasscheibe eine sinnvolle Definitionsmenge für die Länge  x  an.   
D  =   ℝ ⁺ \  0       (keine negativen Lengeneinheiten;  Strecken, Flächen und Volumina können nur positiv sein)

3   Bringe die Seiten  x  und  y  der rechteckigen Glasscheibe in einen funktionalen Zusammenhang.        ------- --Aufstellung der Nebenbedingungen                  noch keine Lösung

4  Stelle die Flächenfunktion der Glasscheibe unter Verwendung der Nebenbedingung aus Aufgabe 3 in Abhängigkeit von der Seite 1 der Glasscheibe dar.
Bestimmung der Zielfunktion mit einer Variablen               noch keine Lösung

5  Berechne die Länge  x  der rechtwinkligen Glasscheibe so, dass seine Fläche maximal wird.
Bestimmung der  relativen Extremstellen  bzw. der  absoluten Extremstellen            noch keine Lösung

6  Kann der Glaser einen größeren Flächeninhalt erhalten, wenn er die Scheibe, wie in der zweiten Konstruktion dargestellt, anders anlegt?      Begründe dies rechnerisch.                   noch keine Lösung

Comments

Dankeschön für die Beiträge, das ist schon mal sehr hilfreich.

müsste ich beim weiteren Verlauf der Aufgabe anders vorgehen, wenn ich bei Aufgabe 1 erst die Flächenfunktion in Abhängigkeit von den Seiten  x  und  y  des Rechtecks aufstelle und nicht mit den Seiten  a  und  b  des  Dreiecks anfange?

Answer 1

hi

wir legen den ursprung des koordinatensystems in die spitze des dreiecks.
wir definieren zwei punkte B' und A'. der punkt A' hängt von der position
des punktes B' ab.
aus dem strahlensatz ergibt sich die abhängigkeit:
B'/B = A'/A
A' = A/B B'
wenn also B' entlang x-achse nach rechts verschoben wird,
wandert A' entlang der y-achse nach oben.
aus dieser beziehung bekommen wir die länge x des zu optimierenden rechtecks:
x^2 = A'^2 + B'^2
x = √(A'^2 + B'^2)
x = √((A/B B')^2 + B'^2)
wir denken uns zwei weitere punkte, D und E. die beiden punkte D und E wandern
entlang der geraden f(x) = -6/4 x + 6, wenn B' entlang der x-achse verschoben wird.
die seitenlänge y ist der abstand der punkte B' und C, wobei die strecke B'C senkrecht
auf der geraden f(x) steht.
mit diesen angaben können wir eine weitere geradengleichung g(x) bestimmen.
weil g(x) senkrecht zu f(x) ist, können wir die steigung von g(x) aus der beziehung
-6/4 * mg = -1
mg = 4/6.
wenn B' entlang der x-achse nach rechts verschoben wird, bewegt sich auch g(x) nach rechts
und damit auch die nullstelle von g(x).
wir können die funktionsgleichung g(x) bestimmen:
g(x) = 4/6 (x-B')

den punkt C bekommen wir durch gleichsetzen der beiden geradengleichungen:
f(x) = g(x)
-6/4 x + 6 = 4/6 (x-B')
...
xc = 4/13 B' + 36/13
der punkt C ist von B' abhängig und befindet sich an der stelle xc = 4/13 B' + 36/13.
die zugehörige y-koordinate yc bekommen wir durch einsetzen des punktes xc in die
geradengleichung f(x) = -6/4 x + 6.
yc = -6/4 xc + 6
yc = -6/4 (4/13 B' + 36/13) + 6
yc = -6/13 B' + 24/13

daraus bekommen wir die seitenlänge y des zu optimierenden rechtecks:
y^2 = (xc - B')^2 + (yc)^2
y^2 = (4/13 B' + 36/13 - B')^2 + (-6/13 B' + 24/13)^2
y^2 = (-9/13 B' + 36/13)^2 + (-6/13 B' + 24/13)^2
y = √(9/13 B'^2 - 72/13 B' + 144/13)
      
damit sieht die flächenfunktion so aus:
A = x*y = √(A'^2 + B'^2) * √(9/13 B'^2 - 72/13 B' + 144/13)
die fläche hängt von den variablen B' und A' ab. wir schmeißen A' raus:
A = x*y = √((A/B B')^2 + B'^2) * √(9/13 B'^2 - 72/13 B' + 144/13)
die fläche hängt jetzt nur noch von B' und vom gegebenen verhältnis A/B ab,
B' kann die werten von 0 bis B = 4 annehmen.
wir setzen die gegebenen werte A = 6 und B = 4 ein und vereinfachen die flächenfunktion
A = √((A/B B')^2 + B'^2) * √(9/13 B'^2 - 72/13 B' + 144/13)
A = √(((6/4 B')^2 + B'^2) * (9/13 B'^2 - 72/13 B' + 144/13))
A = √(9/4 B'^4 - 18 B'^3 + 36 B'^2)

wir berechnen die erste ableitung(wir leiten nach B' ab)
A' = 9 B'^3 - 54 B'^2 + 72 B'

die erste ableitung setzen wir null und berechnen die extremstellen
9 B'^3 - 54 B'^2 + 72 B' = 0

wir erhalten 3 lösungen
B'1 = 0, B'2 = 2, B'3 = 4

wir prüfen, auf maximum mit hilfe der zweiten ableitung
A'' = 27 B'^2 - 108 B' + 72
A''(0) = 72 > 0, kein maximum
A''(2) = -36 < 0, maximum
A''(4) = 72 > 0, kein maximum

an der stelle B' = 2 ist also das gesuchte maximum.
der flächeninhalt beträgt
A = √(9/4 B'^4 - 18 B'^3 + 36 B'^2)
A = √(9/4 2^4 - 18 2^3 + 36 2^2)
A = 6 FE

Comments

Müsste (laut Skizze) die Hypotenuse, die die beiden Kathetenseiten verbindet, nicht
f(x) = -6/4 x + 4  heißen, da diese Gerade die y-Achse bei  4 schneidet.

Wo kommt der t-Wert  t = 6 her?

Für eine Erläuterung bin ich dankbar.