Bruchterme vereinfachen - aber wie?

Question

Aufgabe:

Vereinfache sowet wie möglich und fasse als Bruch zusammen:

((2x-3)/(x/3-1/2))/((1-1/2 x)/(x-2))

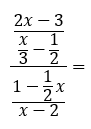
Text erkannt:

\( \frac{\frac{2 x-3}{\frac{x}{3}-\frac{1}{2}}}{\frac{1-\frac{1}{2} x}{x-2}}= \)
Problem/Ansatz:

Problem: Mir fehlt die ausreichend intuitive und anschauliche Vorstellung von Bruchtermen. Beispiel Aufgaben sind immer sehr einfach gehalten und ich kann die Regeln nicht auf komplexe Brüche übertragen (wie in dem Beispiel oben).

Ansatz: Bei Bruchtermen gehe ich immer alle möglichen Operationen durch. Das sind folgende:

- Ausklammern
- Erweitern → Gleichnamig machen für Addition / Subtraktion
- Kürzen (nur Produkte)
- Multiplikation & Division
- Doppelbrüche auflösen a/b / c/d = a*d/b*c
- Umformen
- Binom. Formeln anwenden
- Potenzgesetze

Wenn was fehtl, bitte einen Hinweis geben :)

Binom. Formeln und Potenzen kommen bei uns noch nicht vor.

Rechenweg und Ergebnis der Aufgabe kann ich mir, dank versch. Apps, anzeigen lassen. Das ist also kein Problem aber ich würde das Thema gerne wirklich verstehen. Mit den meisten Aufgaben komme ich super klar, allerdings stehe ich manchmal auf dem Schlauch oder breche eine der Regeln (oft weil ich die "Situation" falsch erkenne bzw. deute). Ich bin echt gut im "nachvollziehen", die Lösungswege sind hinterher immer logisch.

Bei dieser Aufgabe habe ich als erstes den Doppelbruch aufgelöst und dann wollte ich die Nenner gleich machen. Beim Erweitern hat sich mir dann eine Frage gestellt und daran sieht man, dass mir hier noch Verständnis fehlt...

"Problem"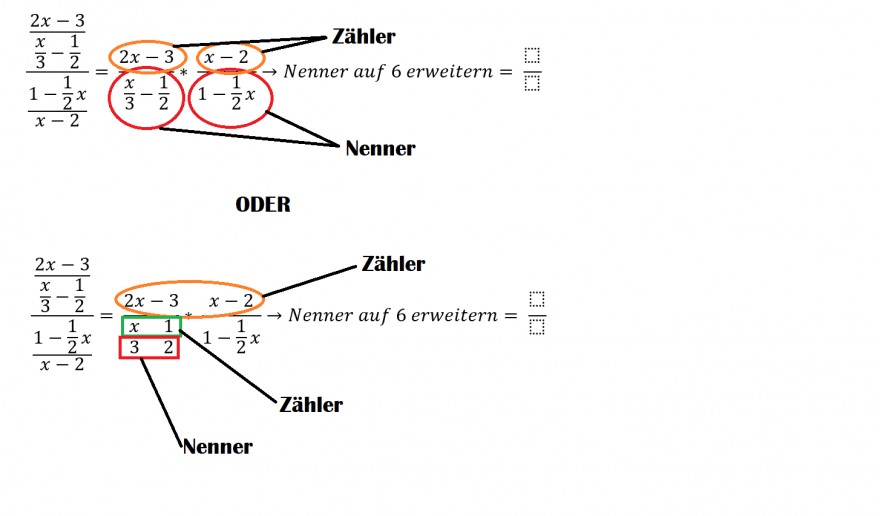

Ich bin mir zu 99% sicher, dass der obere Teil des Bildes stimmt aber solche Verständnisprobleme kommen immer mal wieder vor und dann verhaspel ich mich nur in der Klassenarbeit fehlt mir dann die Zeit.

Habt ihr da nen Tipp für mich?

Nachtrag: Nochmal zu dem Beispiel oben: der zweite Schritt wird ja wahrscheinlich ausklammern beim Term "2x-3" sein. Nur ist das jetzt für mich völlig anders als das Ausklammern z.B. bei "10x-10y". Für mich ist das nicht (direkt) offensichtlich.

Nur um nochmal mein Problem deutlicher aufzuzeigen: ich hab die Möglichkeit des Ausklammerns zuerst nicht erkannt.

Answer 1

Der obere Bruch ergibt gekürzt 6,

der untere -1/2.

6/(-0,5)=-12

:-)

Answer 2

Aloha :)

Wir multiplizieren mit dem Kehrwert, anstatt zu dividieren:$$\phantom{=}\frac{\frac{2 x-3}{\frac{x}{3}-\frac{1}{2}}}{\frac{1-\frac{1}{2} x}{x-2}}=\frac{2 x-3}{\frac{x}{3}-\frac{1}{2}}\cdot\frac{x-2}{1-\frac{1}{2} x}$$

Wir bringen alle Brüche auf den passenden Hauptnenner:$$=\frac{2 x-3}{\frac{2x}{6}-\frac{3}{6}}\cdot\frac{x-2}{\frac{2}{2}-\frac{x}{2}}$$

Wir addieren die Brüche in den Nennern:$$=\frac{2 x-3}{\frac{2x-3}{6}}\cdot\frac{x-2}{\frac{2-x}{2}}$$

Wir multiplizieren mit den Kehrwerten, anstatt zu dividieren:$$=(2x-3)\cdot\frac{6}{2x-3}\cdot(x-2)\cdot\frac{2}{2-x}$$

Wir erweitern den letzten Bruch mit \((-1)\):$$=(2x-3)\cdot\frac{6}{(2x-3)}\cdot(x-2)\cdot\frac{(-2)}{(x-2)}$$

Schließlich können wir kürzen:$$=\cancel{(2x-3)}\cdot\frac{6}{\cancel{(2x-3)}}\cdot\cancel{(x-2)}\cdot\frac{(-2)}{\cancel{(x-2)}}$$Jetzt müssen wir nur noch multiplizieren und sind fertig:$$=6\cdot(-2)=-12$$

Comments

Danke für deine Mühe alles in den Editor einzutippen!

Leider beantwortet das nicht meine Frage, es ging mir eher um den Transfer der Regeln auf andere, komplexe Brüche und meinen Problemen damit.

Allerdings habe ich inzwischen die Antwort auf meine Frage zu dem "Problem"-Bild gefunden: beide Beispiele sind richtig und nicht nur das obere. Habe es mir dann auch selbst bewiesen, indem ich den gleichen Rechenweg wie du gegangen bin.

Ich hab nur ca. 1 h gebraucht, bis ich alles notiert hatte (u.a. weil sehr auführlich und farblich gestaltet) aber selbst 10 min für diese Aufgabe sind schon arg lang imo.

Bin mir momentan auch gar nicht sicher, ob es da überhaupt nen Trick gibt oder ob man einfach üben, üben, üben muss bis es sitzt.

---

Das muss man einfach ein Gefühl für bekommen. Je häufiger man so Mathe-Gymnastik macht, desto eher "sieht" man die nächsten Schritte automatisch vor seinem geistigen Auge.