Integral von f(x,y)=xy über [0,1]x[0,1] berechnen (Gebietsintegral, Analysis)

Question

Aufgabe:

Gegeben ist die Funktion f: ℝ , (x,y) -> f(x,y) = x*y

Integrieren f über dem Gebiet A = [0;1] x [0;1]

I_f (A) = ∫∫ f dA = ...

        A

Answer 1

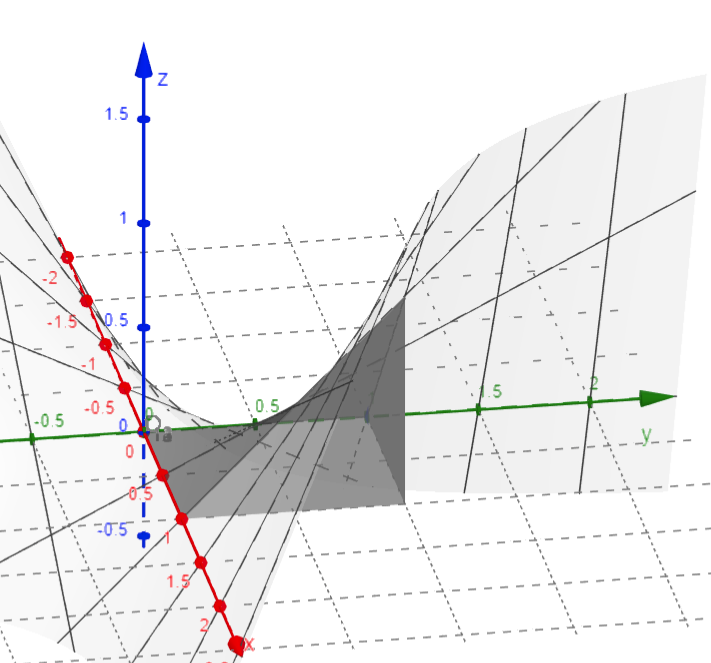
Du kannst nach dem Satz von Fubini selbst entscheiden, in welche Richtung du zunächst integrieren möchtest. Ich habe mich für \(\mathrm{d}x\mathrm{d}y\) entschieden. $$\iint\limits_{[0,1]\times [0,1]}f(x,y)\mathrm{d}x\mathrm{d}y=\int \limits_{0}^{1}\int \limits_{0}^{1}xy \, \mathrm{d}x\mathrm{d}y=\int \limits_{0}^{1}\left[\frac{y}{2}x^2\right]_0^{1}\mathrm{dy}=\int \limits_{0}^{1}\frac{y}{2}\mathrm{dy}=\frac{1}{4}$$