Aloha :)
Das Dreieck hat die Eckpunkte \((0;0)\), \((2;3)\) und \((0;3)\) und sieht so aus:
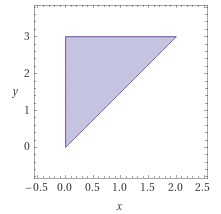
Ein Blick auf den Integranden$$I=\iint\limits_Gx\sin(y^3)\,dx\,dy$$lässt erahnen, dass die Integration über \(dy\) schwierig ist. Daher ist unser Plan, zuerst über \(dx\) zu integrieren, in der "Hoffnung", dass sich dann die nachfolgende Integration über \(dy\) vereinfacht. Das heißt, wir integrieren zuerst bei festgehaltenem \(y\)-Wert entlang der \(x\)-Achse.
Der \(y\)-Wert kann zwischen \(0\) und \(3\) liegen, das heißt: \(y\in[0;3]\). Bei fest gewähltem \(y\) startet der \(x\)-Wert bei \(0\) und endet bei \(\frac23y\), das heißt: \(x\in[0;\frac23y]\).
Damit können wir das Integral konkretisieren:$$I=\int\limits_{y=0}^3\;\int\limits_{x=0}^{\frac23y}x\sin(y^3)\,dx\,dy=\int\limits_{y=0}^3\left[\frac{x^2}{2}\sin(y^3)\right]_{x=0}^{\frac23y}dy=\int\limits_{y=0}^3\frac{2}{9}y^2\sin(y^3)\,dy$$Niun ist die Integration über \(dy\) geschenkt, weil die innere Ableitung \(3y^2\) als Faktor auftaucht:$$\phantom I=\frac{2}{27}\int\limits_{y=0}^3 3y^2\sin(y^3)\,dy=\frac{2}{27}\left[-\cos(y^3)\right]_{y=0}^3=\frac{2}{27}\left(1-\cos(27)\right)\approx0,0957$$