G ist eine Ursprungsgerade parallel zu h

Question

Aufgabe:

… Guten Nachmittag ,

Die Gerade H hat die Gleichung f(x)=2/3x +2

Geben sie die Gleichung von g an.

a) g ist eine Ursprungsgerade parallel zu h

B) Die gerade G schneidet h auf der x Achse und geht durch A(4/-2)

Problem/Ansatz:

… a) der Scheitelpunkt der gerade g ist S(0/0) , da es eine ursprungsgerade ist ,aber auch die Steigung ist gleich wie bei h, da es parallel ist.

b) diese teilaufgabe verwirrt mich , da ich eigentlich schon die Gleichung aufstellen kann , aber wie kann es sein das 2 Parallelen sich auf der x Achse schneiden ,ich hab auch gezeichnet und trotzdem verstehe ich es nicht. Wäre sehr dankbar über eine mögliche Erklärung.

Answer 1

Hallo,

willkommen in der Mathelounge!

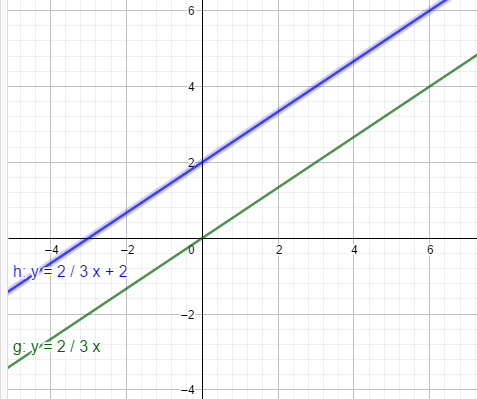
h: \(f(x)=\frac{2}{3}x+2\)

allgemeine Form einer Geradengleichung:

y = mx + b

m = Steigung, b = Schnittpunkt mit er y-Achse

a) Da g durch den Ursprung geht, ist b = 0

gleiche Steigung ⇒ g: \(y=\frac{2}{3}x\)

b) Die Gerade g schneidet h auf der x Achse und geht durch A(4/-2)

Du berechnest den Schnittpunkt von mit der x-Achse:

$$\frac{2}{3}x+2=0\\\frac{2}{3}x=-2\\x=-3$$

Jetzt hast du die beiden Punkte P(-3|0) und A (4|-2). Weißt du, wie man mit zwei Punkten eine Geradengleichung aufstellt?

Gruß, Silvia

Comments

Da g durch den Ursprung geht, ist x = 0

du meinst wohl .. b=0

---

Vielen Dank ! Teilaufgabe a) hatte ich genau so , und bei b) habe ich auch gedacht das ich f(x) = setzen muss , aber ich wusste nicht das es 2 unterschiedliche Geraden sind ,welche ich am Ende berechnen muss .

---

In der Tat! Danke, Wolfgang, ich korrigiere es.

Answer 2

Die Gerade H hat die Gleichung f(x) = 2/3·x + 2

Geben sie die Gleichung von g an.

a) g ist eine Ursprungsgerade parallel zu h

g(x) = 2/3·x

B) Die gerade G schneidet h auf der x Achse und geht durch A(4/-2)

f(x) = 2/3·x + 2 = 0 --> x = -3

Also Gerade durch (-3 | 0) und (4 | -2)

g(x) = (-2 - 0)/(4 - (-3))·(x + 3) + 0 = - 2/7·x - 6/7

Comments

Aber warum haben sie bei der Teilaufgabe 2 als x Wert und nicht 0? Es ist eine Ursprungsgerade , und Ursprungsgeraden gehen ja durch 0 auf der Y Achse.

---

Gut aufgepasst. Sollte natürlich

g(x) = 2/3·x

lauten.

Answer 3

a) g(x) = 2/3* x

g un h haben diesselbe Steigung

b) Schnittstelle:

h(x)= 0

2/3*x+2 =0

x = -3  -> g(-3)=0

Damit hast du 2 Punkte (-3|0] und A, die auf g liegen-

g(x) = m*x+b

m= (-2-0)/(-3-4)= -2/7

0= -2/7*3+b

b= 6/7

g(x) = -2/7*x +6/7