Welche Ursprungsgerade h schneidet die Kostenkurve in x=20

Question

Gegeben ist die Kostenfkt: K(x)=0,025x^2+2x+160

X größer als 0

Welche Ursprungsgerade h schneidet die Kosten Kurve in x=20

In welchem Bereich verläuft die gerade h oberhalb der Parabel

Kann mir bitte hierbei jemand die Vorgehensweise erklären?

Answer 1

beliebige Ursprungsgerad:  g(x) = m * x

f(x) mit K(x) schneiden:    K(x) = g(x)

0,025x²+2x+160 = m*x

x=20 einsetzen:

0,025·20² + 2·20 + 160 = m·20

210 = 20m

m = 210/20 = 21/2 = 10,5

gesuchte Ursprungsgerade:  g(x) = 10,5·x

alle Schnittstellen von K(x) und g(x):

0.025·x² + 2·x + 160 = 10.5·x      | - 10,5x  | : 0,025

x² - 340·x + 6400 = 0

x² + px + q = 0

pq-Formel:  p = - 340  ; q = 6400

x_1,2 = - p/2 ± \(\sqrt{(p/2)^2 - q}\)

....

x₁ = 320   ;  x₂ = 20

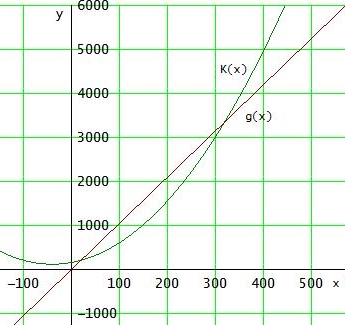
Die Gerade verläuft also für 20 < x < 320 oberhalb der Parabel

Gruß Wolfgang

Answer 2

K(x) = 0.025·x^2  + 2·x + 160

K(20) = 210

Welche Ursprungsgerade h schneidet die Kosten Kurve in x=20

Die Ursprungsgerade lautet

f(x) = 210/20·x

In welchem Bereich verläuft die gerade h oberhalb der Parabel

0.025·x^2  + 2·x + 160 < 210/20·x --> 20 < x < 320