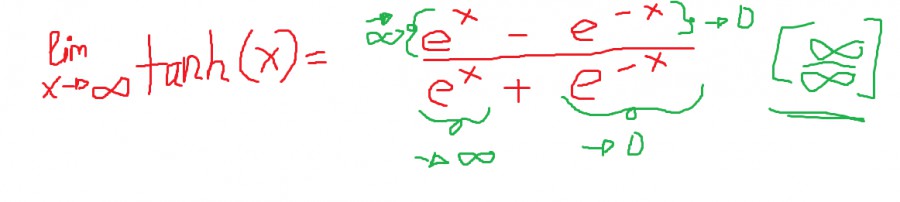Ist es richtig, dass die Funktion tanh(1/x^3) ungerade ist und bei x=0 eine unbehebbare Unstetigkeitsstellle hat?

Question

Wie kann man das Monotonieverhalten (fallend, steigend auf bestimmten Intervallen) ohne Graph mathematisch beschreiben? (ohne Ableitung)

Ist es richtig, dass f(0+) und f(0-) nicht existieren?

Comments

Hilft dir der Graph hier schon mal etwas ?  https://www.wolframalpha.com/input/?i=tanh%281%2Fx%5E3%29

Answer 1

Hilft dir der Graph hier schon mal etwas ?  https://www.wolframalpha.com/input/?i=tanh%281%2Fx%5E3%29

f(0+) und f(0-) könnte gemäss Graph existieren
Grund

Denn Limes tanh (x) für x gegen + unendlich ist +1 und
Limes tanh (x) für x gegen - unendlich ist -1

Da 1/x^3 gegen unendlich geht für x gegen 0+ selbstgegen + unendlich
tanh davon gegen + 1.

Daher gilt f(0+) = 1/1 = 1.

Analog: f(0-) = -1

Kontrolle: Graph.

Ist es richtig, dass die Funktion tanh(1/x³) ungerade ist und bei x=0 eine unbehebbare Unstetigkeitsstellle hat?

Das sehe ich auch so. 

Comments

danke für die Antwort.

Ich verstehe nicht wie man bei f(0+) auf 1 kommt als Grenzwert.

e^unendlich ergibt doch unendlich.

Und e^minus_unendlich ergibt minus unendlich.

Wie kommt dann auf 1/1 = +1 ? Ich erhalte über den Bruchstrich und unter dem Bruchstrich Unendlich. Wäre dankbar über eine Erklärung, denn ich erhalte hier nur unbestimmte Ausdrücke.

---

Wie gesagt kommt das direkt daher, dass tanh(x) → 1 für x gegen unendlich.

Vlg. https://www.wolframalpha.com/input/?i=tanh%28x%29

Solltest du den Verlauf von tanh(x) nicht voraussetzen dürfen

Benutze vielleicht die Definition: tanh(x):= sinh(x) / cosh(x)

---

Ja das verstehe ich. Wenn ich z.B bei tanh(x) 100 einsetze dann kommt 1 raus.

Den Graph habe ich mir auch schon über GeoGebra und Google angeschaut.

 

Wie kann ich das mathematisch darstellen über die Grenzwertbetrachtung? Ich habe ein Bild von meinem Problem angehängt, da komme ich leider nicht weiter und kriege 1/1 nicht raus ....

Es kommt nur Unendlich/Unendlich raus und das ist Unbestimmt und nicht 1/1

---

Teile oben und unten durch e^x

Bruch ist dann:  (1 - e^{-2x})/(1 + e^{-2x})
Nun unendlich einsetzen.

---

Wenn ich kurz mitmischen darf:

Und e^minus_unendlich ergibt minus unendlich.

 

Halt, das ist nicht richtig: e^{-∞} = 1/e^{∞} = 0

(wobei die Schreibung mit ∞ natürlich unschön ist)

---

Ja richtig, ich habe mich kurz vertan beim Nachdenken und konnte nicht mehr bearbeiten. natürlich geht e^minusunendlich gegen 0.

(Das habe ich in meiner Zeichnung wieder korrigiert)
Muss ich bei der Umformung der Funktion die Potenzgesetze anwenden um auf das Ergebnis zu kommen?

---

@Unknown: Besten Dank. Hatte diese Caret-Geschichte nicht begriffen.

@Anonym: Potenzgesetze musst du immer anwenden, wenn du mit Potenzen rechnest.

Meinst du hier:

e^{-x} / e^x = e^{-x} * e^{-x} = e^{-x-x} = e^{-2x} ?

---

Danke für die Antworten. Ich habe bei der Umformung gehangen, dabei musst ich nur die Potenzgesetze anwenden.

EDIT:

Ja genau, aber meinst du nicht  e^-x / e^x = e^-x-x ? Bei Division gleicher Basen kann man durch die Exponenten subtrahieren!

---

Beachte -x-x=-2x

Daher 

e^{-x} / e^x = e^{-x-x}  = e^{-2x}