Hallo liebe Mathelunge nutzer.
Ich habe Schwierigkeiten mit der Lösung folgender Aufgabe:
Berechnen Sie die Umkehrfunktion der Funktion tanh explizit. Setzen Sie dazu die Definition von tanh in die Gleichung \( x=\tanh y \) ein und lösen Sie diese nach \( y \) auf.
Untersuchen Sie weiters den Definitionsbereich dieser Umkehrfunktion, welche mit artanh bezeichnet wird.
Hinweis: Seite 129 im Skriptum zur Vorlesung.
besagte Seite 129 möchte ich euch natürlich auch nicht vorenthalten:
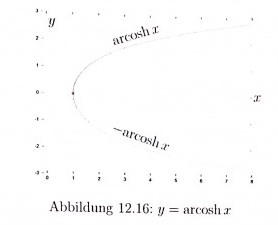
Eine Formel für arcosh x wird durch Auflösen der Gleichung x = cosh y nach y hergeleitet. Man erhält
arcostlı \( x=\ln (x \pm \sqrt{x^{2}-1}) \) x ≥ 1
Dabei ist, präzise gesprochen, der obere (+) Ast von arcosh x die Umkehrfunktion des rechten Astes von cosh x und der untere (-) Ast ist die Umkehrfunktion des linken Astes von cosh x.
Die Funktion tanh \( : \mathbb{R} \rightarrow(-1,1) \) ist auf ganz \( \mathbb{R} \) streng monoton wachsend. Daher existiert eine Umkehrfunktion Area tangens hyperbolicus, die wir mit artanh \( x \) bezeichnen.
Aus \( x=\tanh y, e^{y}=z, x=\frac{z-\frac{1}{z}}{z+\frac{1}{z}}, \) u.s.w. erhalten wir die formelmäßige Darstellung
$$ \text { artanh } x=\frac{1}{2} \ln \frac{1+x}{1-x}, \quad x \in(-1,1) $$
lg und nochmal vielen Dank!