Verschiedene Aufgaben zu quadratischen Funktionen/Termen

Question

1. Beschreibe die Form der durch die Funktionsgleichungen beschreibenen Parabeln und bestimme ihren Scheitelpunkt.

a) \( f(x)=x^{2} \)
b) \( f(x)=-4 x^{2} \)
c) \( f(x)=-3 x^{2}+2 \)
d) \( f(x)=(x-4)^{2}-2 \)
e) \( f(x)=(x+2,5)^{2} \)

2. Stelle für die Graphen eine Funktionsgleichung auf, ohne eine Wertetabelle zu erstellen.

3. Zeichne die Normalparabel mit dem gegebenen Scheitelpunkt und gib ihre Funktionsgleichung an.

a) \( S(0 / 1) \)
b) \( S(-3 / 0) \)
c) \( S(-1 / 3) \)

4. Zeichne die Graphen. Erstelle hierfür eine Wertetabelle.

a) \( y=2 x^{2}-3 \)
b) \( \frac{1}{2} x^{2}+2 \)

5. Multipliziere mittels einer binomischen Formel aus.

a) \( (1,5+4 c)^{2}= \)
b) \( (1+3 b)(1-3 b)= \)
c) \( (3 a-7 b)(3 a+7 b)= \)
d) \( (2-0,1 c)^{2}= \)

6. Faktorisiere mittels einer binomischen Formel.

a) \( 0,64 f^{2}-e^{2}= \)
b) \( 16 a^{2}+8 a b+b^{2}= \)
c) \( 0,25 x^{2}+x+1= \)
d) \( 36 a^{2}+24 a b^{3}+4 b^{2}= \)

Answer 1

Aufgabe 1:

a) f(x) = x²

Normalparabel, nicht verschoben, nicht gestreckt oder gestaucht, nach oben geöffnet, S(0|0)

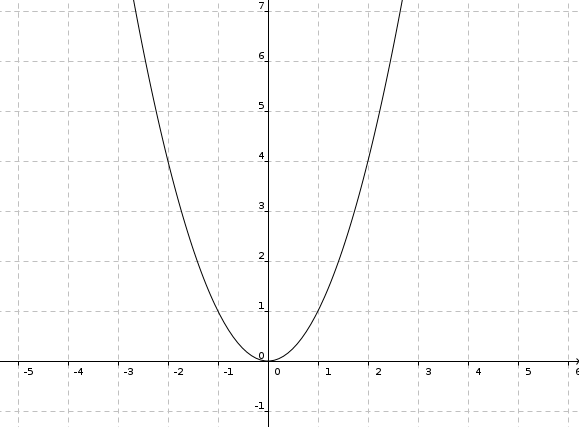
b) f(x) = -4x²

Parabel, mit Faktor 4 gestreckt, nach unten geöffnet, S(0|0)

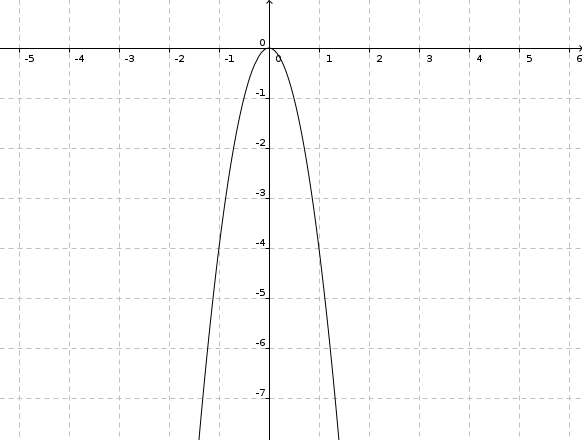
c) f(x) = -3x² + 2

Parabel, mit Faktor 3 gestreckt, nach unten geöffnet, um 2 nach oben verschoben, S(0|2)

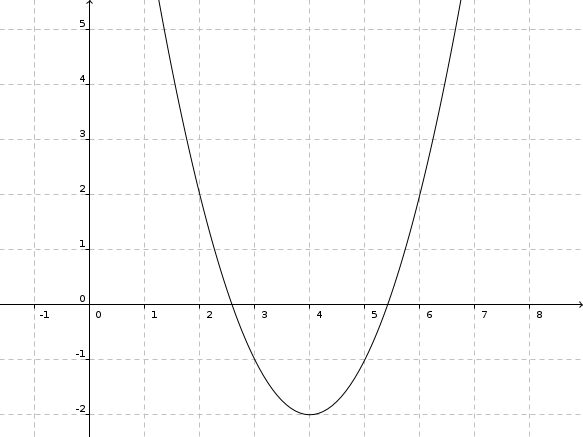
d) f(x) = (x - 4)² - 2

Parabel, nach oben geöffnet, nicht gestreckt oder gestaucht, um 4 nach rechts und um 2 nach unten verschoben, S(4|-2)

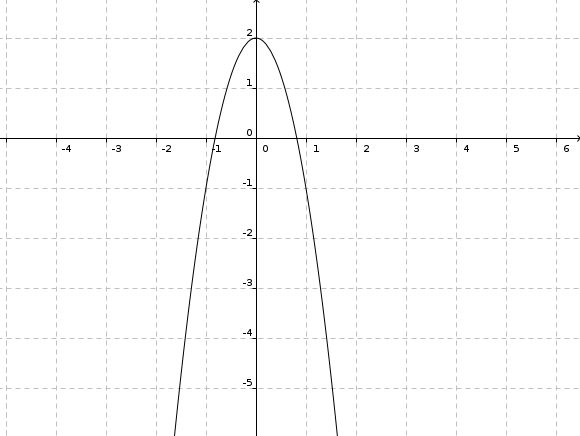
e) f(x) = (x + 2,5)²

Parabel, nicht gestreckt oder gestaucht, nach oben geöffnet, um 2,5 Stellen nach links verschoben, S(-2,5|0)

Damit solltest Du Aufgabe 2 selbst lösen können :-)

3. Zeichne die Normalparabel mit dem gegebenen Scheitelpunkt und gib ihre Funktionsgleichung an.

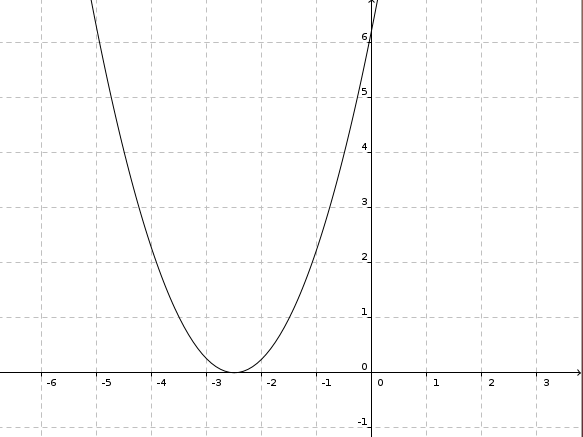
a) S(0|1)

Dies ist die Normalparabel, um eine Stelle nach oben verschoben (wegen der 1), also f(x) = x² + 1

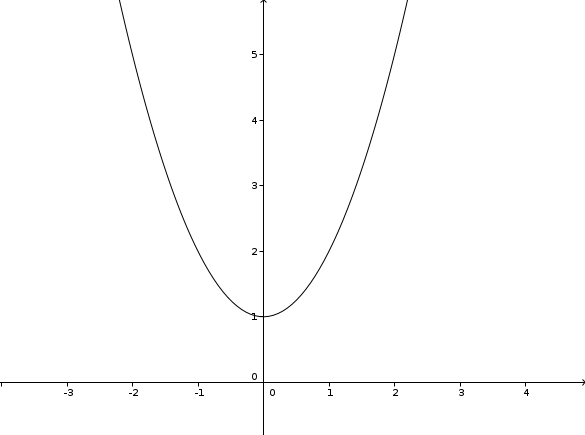
b) S(-3|0)

Dies ist die Normalparabel, um 3 Stellen nach links verschoben (wegen der -3), also f(x) = (x+3)²

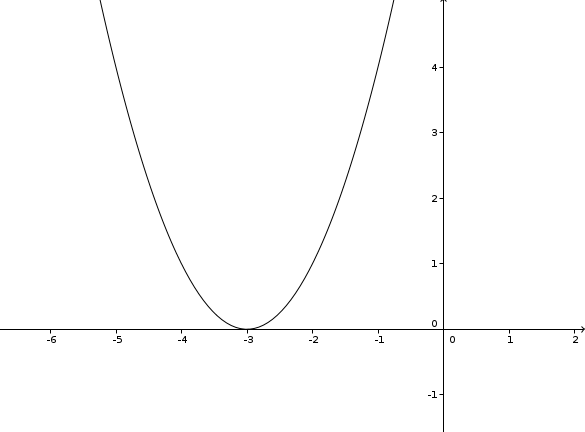
c) S(-1|3)

Normalparabel, um eine Stelle nach links verschoben und um 3 Stellen nach oben, also f(x) = (x+1)² + 3

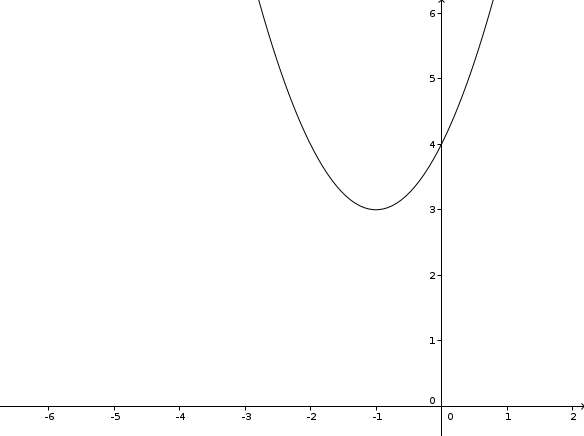
4. Zeichne die Graphen. Erstelle hierfür eine Wertetabelle.

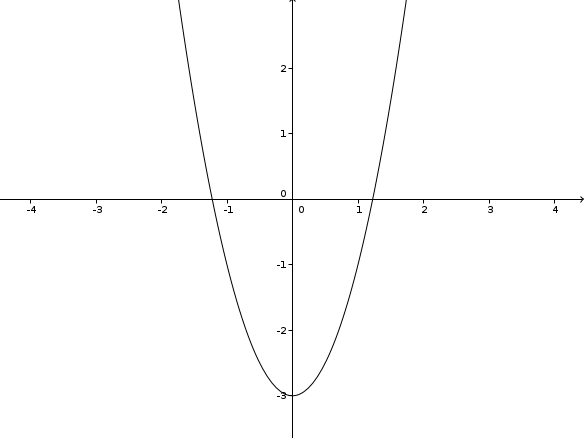
a) y = 2x² - 3

Eine Wertetabelle kannst Du ja wohl selbst erstellen! Du setzt irgendwelche Zahlen für x ein und berechnest nach der Funktionsgleichung den entsprechenden y-Wert, z.B.

x = 1 | y = 2 * 1² - 3 = -1

Die Funktion sieht so aus:

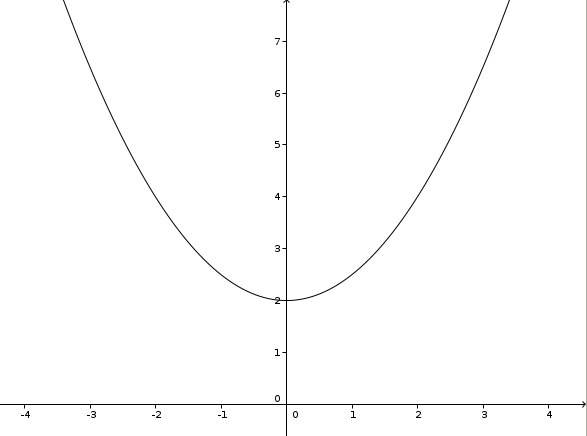
b) 1/2 * x² + 2

5. Multipliziere mittels einer binomischen Formel aus!

a) (1,5 + 4c)²

1. binomische Formel

1,5² + 12c + 16c²

b) (1 + 3b) * (1 - 3b)

3. binomische Formel

1² - 9b²

c) (3a - 7b) * (3a + 7b)

3. binomische Formel

9a² - 49b²

d) (2 - 0,1c)²

2. binomische Formel

4 - 0,4c + 0,01c²

6. Faktorisiere mittels einer binomischen Formel!

a) 0,64f² - e²

3. binomische Formel

(0,8f - e) * (0,8f + e)

b) 16a² + 8ab + b²

1. binomische Formel

(4a + b)²

c) 0,25x² + x + 1

1. binomische Formel

(0,5x + 1)²

36a² + 24ab + 4b²

1. binomische Formel

(6a + 2b)²

Ich hoffe, ich konnte Dir ein wenig helfen!

Zum 2. Aufgabenblatt habe ich jetzt keine Lust mehr :-)

Das kannst Du ja u.U. nochmals als neue Aufgabe posten.

Besten Gruß