Kovexes Viereck Aufgabe der Woche

Question

Aufgabe:

Neue Aufgabe der Woche, die sehr schwierig ist.

Halbierungsprobleme Teil 1

Gegeben ist ein ebenes konvexes Viereck $A B C D$ mit einem beliebigen Punkt $P$ auf der Seite $\overline{C D}$.

Konstruiere eine Gerade durch $P$, die das Viereck in zwei flächengleiche Teile teilt.

Halbierungsprobleme Teil 2

Gegeben ist ein ebenes konvexes Viereck $A B C D$. Konstruiere eine Gerade durch $A$, die das Viereck in zwei flächengleiche Teile teilt.

Halbierungsprobleme Teil 3

Ein spitzwinkliges Dreieck wird durch einen Halbkreis über einer Seite (nach außen) ergänzt. Wie findet man eine Gerade, die diese Figur in zwei flächeninhaltsgleiche Teile zerschneidet?

Halbierungsprobleme Teil 4

Im Dreieck $A B C$ liegt ein beliebiger Punkt $P$ auf der Seite $a=\overline{B C}$. Konstruiere eine Gerade $h$ durch $P$, die das Dreieck in zwei flächeninhaltsgleiche Teile zerlegt und begründe die Konstruktion.

Halbierungsprobleme Teil 5

Konstruiere in einem beliebigen Dreieck $A B C$ eine Parallele zur Seite $c$, so dass zwei flächeninhaltsgleiche Teile entstehen, und begründe die Konstruktion.

Problem/Ansatz:

Bitte die Aufgaben komplett lösen, ich komm gar nicht drauf.

Answer 1

Hallo,

Folgendes ist nicht die vollständige Lösung, aber sollte reichen, dass Du sie Dir erarbeiten kannst. Sonst frage später nochmal nach. Zunächst mal eine Zeichnung:

 

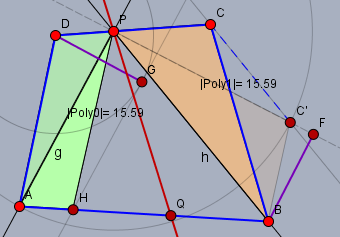
Zeichne zunächst zwei Geraden $g$ und $h$ durch die Punkte $P$ und $A$ und $P$ und $B$ (beide schwarz).

Die Idee ist nun, ein Dreieck $\triangle AHP$ zu konstruieren, so dass die Summe der Flächeninhalte von $\triangle APD$ und $\triangle AHP$ genauso goß ist, wie die Fläche von $\triangle BCP$. Ist der Punkt $H$ konstruiert, so verläuft die gesuchte Gerade durch $PQ$, wobei $Q$ der Mittelpunkt der Strecke $HB$ ist.

Zur Konstruktion von $H$ schere ich das Dreieck $\triangle BCP$ (hellbraun) längst einer Parellelen zu $PB$ durch $C$ (blau gestrichelte Linie), so dass die Strecke $|PC'| = |PA|$ ist. Die Höhe des dadurch entstandenden Dreiecks $\triangle BC'P$ über der Seite $PC'$ ist $|BF|$. Nun fälle ich das Lot von $D$ auf $g$ und trage $|BF|$ in Richtung $g$ auf dem Lot ab. Damit erhalte ich den Punkt $G$. Die Parallel durch $G$ zu $g$ schneidet $AB$ in $H$.

Der Mittelpunkt der Strecke $HB$ ist $Q$ und die Gerade durch $PQ$ teilt das Dreieck $HBP$ in zwei gleich große Teile und somit auch das Viereck $ABCD$.

Du kannst Dir nun selbst überlegen, wann die Konstruktion ihre Grenzen erreicht. Sie funktioniert aber auch dann, wenn die Fläche von $\triangle APD$ größer ist als die von $\triangle BCP$...

Halbierungsproblem Teil 2

ist wie Teil 1, nur dass $P$ jetzt in $A$ liegt. Und entscheide am Anfang, welche der Seiten $BC$ und $CD$ die pasende 'Grundseite' ist, auf der $Q$ liegt.

Halbierungsproblem Teil 3

... dachte erst, das geht mit einer euklidischen Konstruktion gar nicht. Ich habe aber noch eine idee dazu. Es wäre schlauer gewesen, dafür eine eigene Frage hier in der mathelounge einzustellen!

Halbierungsproblem Teil 4

Die Grundidee ist dieselbe wie bei Teil 1 und 2. Ich zeige es mal ohne Kommentar:

Halbierungsproblem Teil 5

... ist zu einfach. Bitte selber nachdenken ;-) Tipp: wie groß ist die Fläche eines Dreiecks, wenn Höhe $h$ und Grundseite $c$ gegeben sind?

Answer 2

Teil 1

$$2F_{APD}=|PD×PA|$$

$$2F_{ABP}=|PA×PB|$$

$$2F_{BCP}=|PB×PC|$$

$$2F_{ABCD}=2F_{APD}+2F_{ABP}+2F_{BCP}$$

Fall 1

$$2F_{ABD}/F_{ABCD}=k≥1$$

$$Q =D+1/k*AD$$

Fall 2

$$2F_{PBC}/F_{ABCD}=k≥1$$

$$Q=C+1/k*CB$$

Fall 3

$$2F_{ABP}/(F_{ABCD}-2F_{APD})=k≥1$$

$$Q=A+1/k*AB$$

$$PQ$$ teilt das Viereck in zwei gleich große Teile.

Teil 2 geht dann entsprechend.