Hallo,
Überlege zunächst, was allgemein der Ausdruck \(|x-a|=d\) besagt. Das sind doch genau die beiden \(x\)-Werte, die von \(a\) den Abstand \(d\) haben.
Demnach ist \(|3+x|\), was das gleiche ist wie \(|x-(-3)|\), der Abstand von \(x\) zu \(-3\). Und wenn dieser genauso groß ist wie der Abstand zu \(5\), so muss das \(x\) genau in der Mitte zwischen \(-3\) und \(5\) liegen:
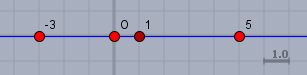
b) kann man umformen zu \(|x-5| \ge |x - (-3)|\), heißt doch, dass \(x\) von \(5\) gleich oder weiter weg sein soll, wie von \(-3\). Also:
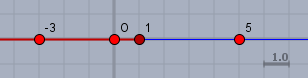
alles, was links von der \(1\) liegt, einschließlich der \(1\), erfüllt diese Bedingung.