Stetigkeit und Differenzierbarkeit (anhand einer Zeichnung)

Question

Aufgabe:

Gegeben sei der nebenstehende Graph einer Funktion.

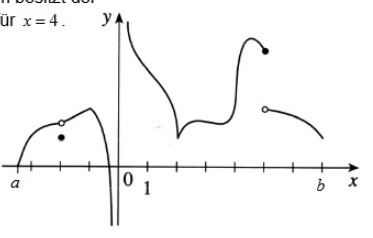
Hinweis: Es gilt: \( f(x) \stackrel{x \rightarrow 0}{\longrightarrow} \pm \infty . \) Außerdem besitzt der Funktionsgraph eine senkrechte Tangente für \( x = 4 \).

a) Für welche Werte von \( x \) ist die Funktion auf \( (a, b) \) nicht stetig?

b) Für welche Werte von \( x \) ist die Funktion auf (a, b) \) nicht differenzierbar?

Hinweis: Aufgabe entnommen aus James Stewart, Calculus, Brooks/Cole 2003

Ich würde sagen x = 0 ; x=5 sind nicht stetig und x=0,x=2,x=5 sind nicht differenzierbar.

Comments

Was ist mit der Stetigkeit bei x = -2 ?

---

Was ist mit der Differenzierbarkeit an den Stellen  x = -1  und  x = 4 ?

---

Was ist nun mit der Differenzierbarkeit bei -2 ? Die Funktion ist bei -2 differenzierbar, korrekt ?

---

Da sie in -2 nicht stetig ist, kann sie auch nicht differenzierbar sein

Answer 1

Nicht stetig für die Werte: -2, 0, 5

Nicht diffb. für die Werte: -2, -1, 0, 2, 5

Comments

Differenzierbar bei  x = 4 ?

---

Falls dieser Bereich eine Senkrechte Steigung aufweist, ist sie dort ebenfalls nicht differenzierbar. Allerdings würde es sich dann nicht mehr um eine Funktion handeln, weil einem x Wert mehrere y-Werte zugeteilt werden würden. Somit ist sie an der Stelle 4 differenzierbar.

---

Im Hinweis steht allerdings, dass es sich um eine senkrechte Tangente handelt, deshalb wird darauf sicherlich ein Punkt vergeben, wenn man 4 als nicht differenzierbar angibt.

---

Warum soll denn  f  keine Funktion sein, wenn der Funktionsgraph an der Stelle  x = 4  eine senkrechte Tangente aufweist? Allenfalls ist dann besagte Tangente keine Funktion.

---

Damit die Tangente senkrecht ist, muss der Graph an der Stelle ebenfalls senkrecht sein. Oder seh ich das falsch?

---

Nicht der Funktionsgraph ist senkrecht, sondern die Tangente. Es existiert ein eindeutiger Funktionswert  f(4).