a)
f(x) = \( \frac{1}{9} \)•(3x + 2)^3
f´(x)=3• \( \frac{1}{9} \) (3x + 2)^2 • 3= (3x + 2)^2
f´(2)= (3•2 + 2)^2 = 64
b)
(3x + 2)^2 = 0
3x+2=0
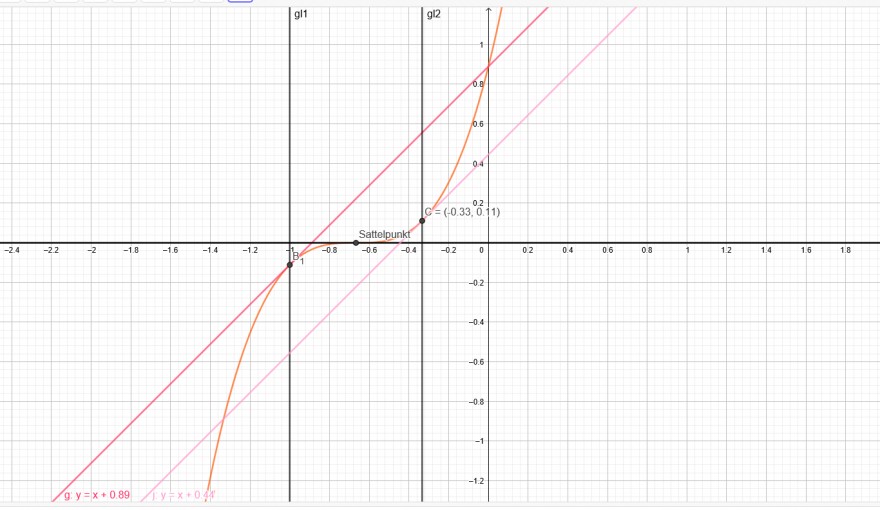
Sattelpunkt: x= - 2/3 → f(- \( \frac{2}{3} \) )=0 →x- Achse ist Tangente, somit gibt es keine Tangente parallel zur x Achse.
c)
(3 x + 2 )^2 = 1
1.) (3x + 2)=1
x= -\( \frac{1}{3} \)→ y = \( \frac{1}{9} \)
2.) (3 x + 2) = - 1
x = - 1 → y = - \( \frac{1}{9} \)
mfG
Moliets